Bases de données relationnelles et normalisation :
de la première à la sixième forme normale
Date de publication : 07/09/2008. Date de mise à jour : 14/07/2012.
4. Quatrième forme normale
4.1. Au-delà de la BCNF
4.2. Observations à propos de la jointure naturelle
4.3. Dépendance multivaluée (DMV)
4.4. Décomposition sans perte de données. Premier théorème de Fagin
4.5. Dépendance fonctionnelle et dépendance multivaluée (règle de réplication)
4.6. Dépendance multivaluée triviale
4.7. Quatrième forme normale (4NF)
4.8. Un (sympathique) théorème de Date et Fagin concernant la 4NF
4.9. 4NF et relvars « toutes clés », une légende à détruire
4.10. La 4NF et Merise
4.11. Merise et la chasse aux ternaires
4.12. Observations concernant la décomposition des relvars
4.13. Approche ascendante vs approche descendante
4.14. Implication de la BCNF par la 4NF
4. Quatrième forme normale
4.1. Au-delà de la BCNF
Bien que la normalisation en BCNF permette d'éliminer des wagons de redondances parasitant les relations,
avec en prime la disparition dans la foulée d'un cortège de problèmes de mise à jour inhérents, il reste
malgré tout des cas de redondance face auxquels la BCNF se révèle impuissante. En 1976-1977, Claude Delobel,
Carlo Zaniolo et Ronald Fagin découvrirent chacun de leur coté un nouveau type de dépendance, à savoir
la dépendance multivaluée (DMV), qui fut à la base de nouvelles techniques pour décomposer des
relations réputées jusque-là « incassables » et éliminer ainsi des redondances et anomalies
rebelles. En 1977 Fagin donna l'énoncé de la quatrième forme normale (4NF), nous permettant de nous assurer
que les tables infectées par ces redondances auront été assainies après normalisation (cf. [Fagin 1977]).
Mais avant de traiter des dépendances multivaluées et de la 4NF, faisons d'abord un détour du côté de
la modélisation des données.
4.2. Observations à propos de la jointure naturelle
Intéressons-nous aux ingénieurs spécialistes en bases de données de la SARL Les Prévoyants de l'Avenir
des Bases de Données (LPABDD, filiale de DVP), plus précisément en ce qui concerne les projets auxquels
ils ont été affectés au fil du temps, outre leurs compétences concernant les SGBD.
Les règles de gestion qui nous intéressent ici sont les suivantes :
Exemples :
| |
Albert maîtrise IMS et DB2. Il a été affecté au projet Biglotron en 2003, 2004 et 2006.
Il a aussi été affecté au projet Slalom en 2003 et 2005.
Bernard maîtrise BS12 et DB2. Il a été affecté au projet Biglotron en 2004 et 2005.
Charles maîtrise Oracle. Il a été affecté au projet TantkYoradla en 2007 et 2008.
|
Sous forme prédicative (un prédicat dyadique de la forme Fxy et un prédicat
triadique de la forme Gxyz ) :
(P1)
Fxy : L'ingénieur IngId maîtrise le SGBD SgbdId
(P2)
Gxyz : L'ingénieur IngId a été affecté au projet ProjId
au cours de l'année Annee
Une représentation graphique :
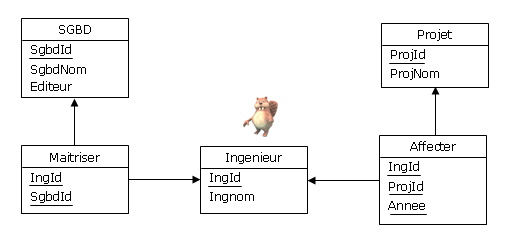
Figure 4.1 - Les ingénieurs, leurs SGBD, leurs projets
Un instantané (relations à un moment donné, ou contenu des tables au sens SQL). Les clés sont soulignées :
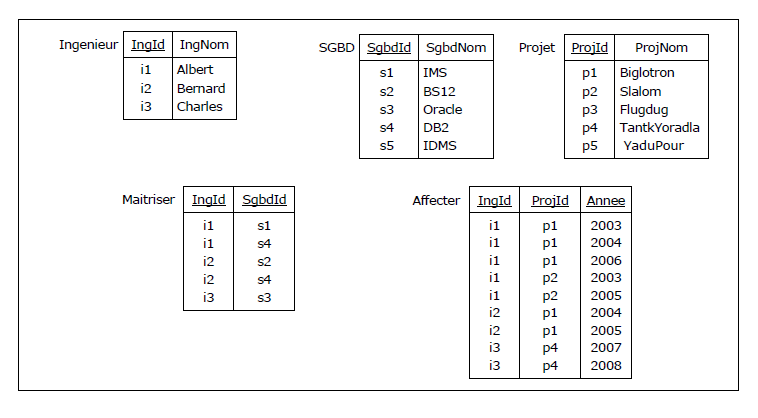
Figure 4.2 - Les ingénieurs, leurs SGBD, leurs projets (instantané)
On vérifie sans difficulté que la BCNF est partout vérifiée. Supposons maintenant que l'on mette
en oeuvre une relvar virtuelle (vue), appelons-la ISPV, jointure naturelle des relvars Affecter
et Maitriser. La consultation de la relvar donne lieu au résultat suivant :
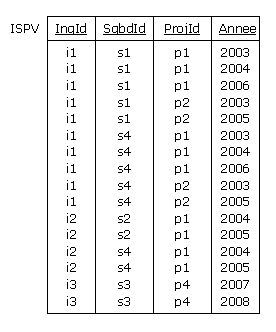
Figure 4.3 - ISPV : Jointure naturelle des tables Maitriser et Affecter
En Tutorial D, la définition de la relvar est la suivante :
VAR ISPV
VIRTUAL
(Maitriser JOIN Affecter)
KEY {IngId, SgbdId, ProjId, Annee} ;
|
En SQL :
CREATE VIEW ISPV (IngId, SgbdId, ProjId, Annee)
AS SELECT a.IngId, a.SgbdId, b.ProjId, b.Annee
FROM Maitriser
AS a
INNER JOIN Affecter
AS b
ON a.IngId = b.IngId ;
|
Notons en passant que ce que l'on a pour habitude d'appeler vue est en réalité une relvar,
virtuelle certes, mais relvar quand même, d'où la présence de la clause KEY accompagnant la
définition de la relvar (en Tutorial D tout du moins).
Observations
Le quadruplet {IngId, SgbdId, ProjId, Annee}, c'est-à-dire l'ensemble des attributs de la relvar
ISPV en constitue la clé. En effet, aucun triplet d'attributs ne vérifie la règle d'unicité des
clés candidates. Par exemple :
Pour le triplet {IngId, SgbdId, ProjId} et pour le tuple <i1, s1, p1>, on a 3 années
distinctes : 2003, 2004, 2006.
Pour le triplet {IngId, SgbdId, Annee} et pour le tuple <i1, s1, 2003>, on a 2 projets
distincts : p1, p2.
Pour le triplet {IngId, ProjId, Annee} et pour le tuple <i1, p1, 2004>, on a 2 SGBD
distincts : s1, s4.
Pour le triplet {SgbdId, ProjId, Annee} et pour le tuple <s4, p1, 2004>, on a 2 ingénieurs
distincts : i1, i2.
|
-
La relvar ISPV respecte la BCNF
|
En effet, toutes les dépendances fonctionnelles qui lui sont associées sont triviales.
|
-
Piège de la connexion (connection trap)
Le prédicat associé à ISPV est la conséquence d'une jointure naturelle, il est donc la conjonction
des prédicats P1 et P2 (en relationnel : P1 AND P2) :
(P1 ET P2) :
L'ingénieur IngId maîtrise le SGBD SgbdId ET
il a été affecté au projet ProjId au cours de l'année Annee.
Le piège mortel serait de le confondre avec le prédicat tétradique suivant :
(P3)
Hxyzw : L'ingénieur IngId a utilisé le SGBD SgbdId dans le
cadre du projet ProjId au cours de l'année Annee
Selon lequel on énoncerait des contre-vérités, du genre « Albert a utilisé IMS dans le cadre
du projet Biglotron » (ce qu'Albert niera farouchement !) Toutefois, si le prédicat P3 devait
exprimer une règle de gestion authentique, alors il faudrait appeler un chat un chat et
mettre en oeuvre une relvar de base, telle que la relvar Utiliser ci-dessous, de prédicat P3,
cette fois-ci non dérivable, donc sans piège :
|
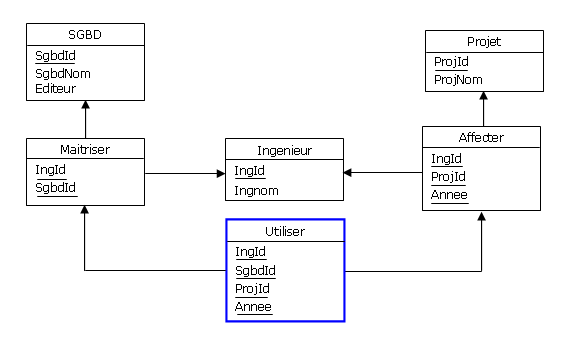
Figure 4.4 - Quels ingénieurs ont utilisé quels SGBD pour quels projets
Une fois la relvar Utiliser valorisée par qui de droit, on constaterait qu'Albert n'a effectivement
pas utilisé IMS dans le cadre du projet Biglotron. Par contraste avec ISPV, la relvar Utiliser
n'exprime que la réalité (hypothèse du monde clos) :
|
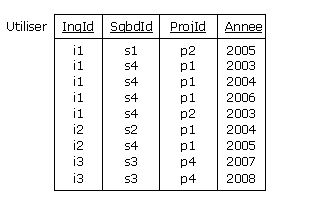
Figure 4.5 - Utilisation effective des SGBD dans le cadre des projets
|
Pour en revenir à la relvar ISPV, on voit qu'elle est particulièrement redondante.
En effet, pour chaque ingénieur qui y figure, et pour chaque SGBD qu'il maîtrise,
est systématiquement fourni l'ensemble de ses affectations aux projets, et de la même façon,
pour chacune de ses affectations, la relvar fournit l'ensemble des SGBD qu'il maîtrise.
|
|
Cette gabegie est choquante eu égard au principe même de la normalisation dont un des principaux
objets est quand même l'élimination de redondances non voulues. Pire, dans ISPV le mensonge est en
embuscade et imaginons que, horresco referens ! lors de l'étape de conception de la base
de données nous ayons fait d'ISPV une relvar de base
ou une table au sens SQL... Nous devrons tout mettre en œuvre pour repérer et éradiquer
ces redondances. A cette fin, nous devons savoir manier les outils nécessaires,
à savoir les dépendances fonctionnelles bien sûr, mais aussi et surtout ceux qu'on appelle
les dépendances multivaluées.
|
4.3. Dépendance multivaluée (DMV)
Considérons une relvar R {X, Y, Z} dans laquelle X, Y et Z représentent des sous-ensembles d'attributs
de l'en-tête H de R (avec Z = H — X — Y,
c'est-à-dire l'ensemble des attributs appartenant à H mais ni à X ni Y).
Si pour chaque valeur prise par X,
les valeurs prises par Y sont indépendantes
des valeurs prises par Z, il existe alors ce qu'on appelle une dépendance multivaluée, notée
X ➔➔ Y.
(A signaler que X et Y ne sont pas nécessairement disjoints). Plus précisément :
Illustrons ceci avec l'exemple de la relvar ISPV. Étant la jointure naturelle des relvars Maitriser et
Affecter, indépendantes l'une de l'autre du fait des règles de gestion initiales,
la relvar ISPV est
ipso facto affectée des dépendances multivaluées (DMV) suivantes :
.jpg)
DMV1 : {IngId} ➔➔ {SgbdId}
Ce qui se lit : {SgbdId} est
multi-dépendant de {IngId}, ou encore
{IngId}
multi-détermine {SgbdId} ;
.jpg)
DMV2 : {IngId} ➔➔ {ProjId, Annee}
{ProjId, Annee} est multi-dépendant de {IngId},
{IngId} multi-détermine {ProjId, Annee}.
En effet, la jointure naturelle « Maitriser JOIN Affecter »
(cas de l'ingénieur s1 en l'occurrence) donne lieu aux tuples :
t1 = <i1, s1, p1, 2003> et t2 = <i1, s4, p2, 2003>
mais aussi aux tuples :
t3 = <i1, s1, p2, 2003> et
t4 = <i1, s4, p1, 2003>
De même, la jointure naturelle donne lieu aux tuples :
t5 = <i1, s1, p1, 2004> et t6 = <i1, s4, p1, 2006>
mais aussi aux tuples :
t7 = <i1, s1, p1, 2006> et
t8 = <i1, s4, p1, 2004>
Etc., etc., etc.
De la sorte, alors que quel que soit l'ingénieur, les SGBD qu'il maîtrise n'ont rien à voir avec ses
affectations à des projets, via ISPV on arrive à rendre mutuellement dépendantes les compétences et
les affectations de cet ingénieur, et le piège de la connexion se referme comme on l'a vu.
Supposons maintenant que le système évolue et que l'on ait à mettre œuvre la règle de gestion selon
laquelle on doit savoir quels SGBD ont été mis en œuvre par quels ingénieurs
dans le cadre de quels projets : cette fois-ci, il n'y a plus indépendance entre les compétences
et les affectations et il devient nécessaire de mettre en œuvre la relvar de base Utiliser
(cf. Figure 4.4). A défaut, horresco referens à nouveau..., si l'on transformait
ISPV elle-même en relvar de base (ou en table SQL), la validité en serait compromise,
et à moins de parfaitement maîtriser le sujet des dépendances multivaluées et de prendre
les précautions qui s'imposent, qui se soucierait d'assurer la pérennité de DMV1 et DMV2 lors des
opérations de mise à jour portant sur cette relvar ?
4.4. Décomposition sans perte de données. Premier théorème de Fagin
La définition de la dépendance multivaluée sous-entend que si l'on effectue la projection de la relvar
ISPV sur les attributs {IngId, SgbdId} d'une part et {IngId, ProjId, Annee}
d'autre part, alors cette décomposition est sans perte de données, c'est-à-dire que la jointure naturelle de ces
deux projections redonne très exactement ISPV. De fait, cette relation entre dépendance multivaluée et
décomposition sans perte existe bien et fait l'objet du théorème suivant, dû à Ronald Fagin (dans le cadre de cet
article, nous l'appellerons le Premier théorème de Fagin, cf. [Fagin 1977]) :

(A noter qu'à partir de la jointure de R1 {X, Y} et R2 {X, Z} on infère la DMV
X ➔➔ Y, alors qu'avec le théorème de Heath (cf. paragraphe 3.3.2),
à partir de cette jointure on ne peut pas inférer la DF X ➔ Y pour R,
DF qui peut donc être perdue quand on normalise en BCNF alors qu'elle exprimerait une règle
de gestion, cf. paragraphe 3.7).
On peut encore formuler ainsi le Premier théorème de Fagin ([Date 2004]) :
Comme Y et Z jouent un rôle symétrique, on peut formuler la règle dite de complémentation :
Quant à la notation, au lieu d'écrire :
{IngId} ➔➔ {SgbdId}
{IngId} ➔➔ {ProjId, Annee}
On peut écrire de façon plus ramassée :
{IngId} ➔➔ {SgbdId} | {ProjId, Annee}
4.5. Dépendance fonctionnelle et dépendance multivaluée (règle de réplication)
Reprenons la définition de la dépendance multivaluée :
|
Soit une relvar R {X, Y, Z} où X, Y et Z représentent des sous-ensembles d'attributs de l'en-tête H de R
(X et Y ne sont pas nécessairement disjoints).
Étant donnés <x, y, z> et <x,
y ,
z ,
z >
deux tuples appartenant à R, la dépendance multivaluée
X ➔➔ Y est vérifiée si et seulement si les tuples
<x,
y >
deux tuples appartenant à R, la dépendance multivaluée
X ➔➔ Y est vérifiée si et seulement si les tuples
<x,
y ,
z> et <x, y,
z ,
z> et <x, y,
z >
appartiennent aussi à R. >
appartiennent aussi à R.
|
Maintenant, si une relvar R vérifie la dépendance fonctionnelle X ➔ Y, alors pour tous
les tuples <x, y, z> et <x,
y

,
z

>
de R, on a y = y

. Il s'ensuit que
la condition d'existence des tuples <x,
y

,
z> et <x, y,
z

> est
de facto vérifiée,
en vertu de quoi la dépendance multivaluée X ➔➔ Y est vérifiée elle aussi,
ce qui donne lieu à la règle dite de
réplication :
Si X ➔ Y alors X ➔➔ Y.
4.6. Dépendance multivaluée triviale
Le concept de dépendance multivaluée triviale (c'est-à-dire toujours vérifiée) est à définir,
car elle intervient dans la définition de la 4NF.
Soit X et Y deux sous-ensembles d'attributs de l'en-tête H d'une relvar R.
La dépendance multivaluée X ➔➔ Y est triviale si et seulement si :
-
Y est un sous-ensemble de X ;
-
Ou encore si H est l'union de X et de Y (au sens de la théorie des ensembles).
Par exemple, si H est composé des trois attributs
A, B et C,
et si les DMV {A} ➔➔ {B} et {A} ➔➔ {C}
sont vérifiées, elles ne sont pas triviales contrairement à la DMV {A, B} ➔➔ {C}.
A noter que si la DMV {A} ➔➔ {B} | {C} est triviale,
alors {B} ou {C} est l'ensemble vide {}.
4.7. Quatrième forme normale (4NF)
On peut maintenant donner l'énoncé de la quatrième forme normale (4NF), dû à Ronald Fagin ([Fagin 1977]) :
 |
A relation schema R* is in fourth normal form (4NF) if, whenever a nontrivial multivalued dependency
X ➔➔ Y holds for R*, then so does the functional dependency X ➔ A
for every column name A of R*.
|

Pour faire le parallèle avec la définition donnée de la BCNF par Zaniolo (cf. paragraphe 3.3.1),
on peut encore écrire :
 |
Soit R une relvar et X et Y des sous-ensembles d'attributs quelconques de l'en-tête H de R.
R est en quatrième forme normale (4NF) si et seulement si,
pour chaque dépendance multivaluée X ➔➔ Y vérifiée
pour R, au moins une des conditions suivantes est satisfaite :
.jpg) √ Cette dépendance multivaluée est triviale.
√ Cette dépendance multivaluée est triviale.
.jpg) √ La dépendance fonctionnelle X ➔ {A} est vérifiée pour chaque
attribut A de H (X est alors une surclé de R).
√ La dépendance fonctionnelle X ➔ {A} est vérifiée pour chaque
attribut A de H (X est alors une surclé de R).
|
Illustration :
Considérons à nouveau l'instantané de la relvar ISPV (Figure 4.3), comportant comme on l'a vu les dépendances
multivaluées non triviales (cf. paragraphe 4.3) :
.jpg)
DMV1 : {IngId} ➔➔ {SgbdId}
.jpg)
DMV2 : {IngId} ➔➔ {ProjId, Annee}
Nonobstant les périls inhérents évoqués au paragraphe 4.3, imaginons que, toute honte bue, de cette
relvar piège nous fassions une relvar de base (table en SQL), appelons-la ISP. Cette relvar vérifie la BCNF car
les dépendances fonctionnelles sont toutes triviales. En revanche, la 4NF est violée. En effet, le multi-déterminant
{IngId} des deux DMV n'est pas surclé de la relvar puisque, comme on l'a vu précédemment avec ISPV, ISP n'a qu'une
seule surclé, le quadruplet {IngId, SgbdId, ProjId, Annee} (clé primaire au sens SQL).
Mais en vertu du 1er théorème de Fagin, la relvar ISP est décomposable sans perte de données,
elle n'a donc pas lieu d'exister.
A cette occasion, on peut aussi se servir du théorème suivant, que l'on retrouve par exemple chez Ullman
(cf. [Ullman 1982], « Theorem 7.2 ») :
non_indente.jpg) |
Si ρ = (R1, R2) est une décomposition de R, et D un ensemble de
dépendances fonctionnelles et multivaluées associé à R, alors ρ préserve le contenu de la base de données
par rapport à D si et seulement si on vérifie
(R1  R2) ➔➔ (R1 — R2)
ou (R1 R2) ➔➔ (R1 — R2)
ou (R1  R2) ➔➔ (R2 — R1). R2) ➔➔ (R2 — R1).
|
En posant R1 = {IngId, SgbdId} et R2 = {IngId, ProjId, Annee},
R1

R2 est égal à {IngId} et R1 — R2
est égal à {SgbdId}. Comme la DMV {IngId} ➔➔ {SgbdId} est donnée, on vérifie bien
(R1

R2) ➔➔ R1 — R2,
donc la relvar ISP est décomposable sans perte de données, et l'on retrouve ainsi les relvars Maitriser
et Affecter (cf. figure 4.2).
Si la relvar ISP viole la 4NF mais est décomposable selon les relvars Maitriser et Affecter (voir toutefois
les réserves faites au paragraphe 4.12), on observera pour leur part que ces deux dernières respectent la 4NF ;
c'est vrai en ce qui concerne la relvar Maitriser {IngId, SgbdId} car ses DMV sont toutes triviales,
{IngId} ➔➔ {SgbdId} et {SgbdId} ➔➔ {IngId} en particulier.
A son tour, pour que la relvar Affecter ne vérifie pas la 4NF, il faudrait qu'il existe une des dépendances
multivaluées non triviales suivantes :
.jpg)
DMV1 : {IngId} ➔➔ {ProjId} | {Annee}
.jpg)
DMV2 : {ProjId} ➔➔ {IngId} | {Annee}
.jpg)
DMV3 : {Annee} ➔➔ {IngId} | {ProjId}
Mais, conséquence des règles de gestion, ça n'est pas le cas (cf. Figure 4.2).
En effet, concernant DMV1, la présence des deux tuples :
<i1, p1, 2004> et <i1, p2, 2003> devrait entraîner la présence du tuple <i1, p2, 2004>,
lequel manque bien sûr à l'appel.
De la même façon, concernant DMV2, la présence des deux tuples :
<i1, p1, 2003> et <i2, p1, 2004> devrait entraîner la présence du tuple <i2, p1, 2003>
qui lui aussi est absent.
Et, concernant DMV3, la présence des deux tuples :
<i1, p2, 2005> et <i2, p1, 2005> devrait entraîner la présence du tuple <i2, p2, 2005>
qui lui aussi fait défaut.
Conclusion : la table Affecter vérifie la 4NF (et du même coup la BCNF, cf. paragraphe 4.14).
4.8. Un (sympathique) théorème de Date et Fagin concernant la 4NF
Si une relvar R vérifie la BCNF et si elle est munie d'au moins une clé mono-attribut,
alors elle vérifie la 4NF.
|
Ce théorème permet de se rendre compte qu'on peut facilement se faire piéger lors de la conception
d'une base de données. Supposons en effet que le prédicat P3 : « L'ingénieur IngId a utilisé
le SGBD SgbdId dans le cadre du projet ProjId au cours de l'année Annee »
fasse l'objet d'une règle de gestion (cf. paragraphe 4.2), et qu'au lieu de la relvar Utiliser
(cf. figure 4.4), on mette en oeuvre la relvar piège ISP d'en-tête
{IngId, SgbdId, ProjId, Annee} (cf. paragraphe 4.7), dont le prédicat est en réalité
la conjonction des prédicats P1 et P2.
ISP a elle aussi pour clé le quadruplet {IngId, SgbdId, ProjId, Annee}.
Maintenant, certains concepteurs et DBA ont pour
principe qu'en SQL toute clé primaire doit être singleton (mono-attribut) :
on ajoute alors à l'en-tête d'ISP un attribut, nommons-le IspId, servant pour la clé primaire
(symbolisée ci-dessous par un double soulignement). Le quadruplet {IngId, SgbdId, ProjId, Annee}
est ravalé de facto au rang de clé alternative. Le contenu de la table SQL correspondante,
nommons-la ISP2, est le suivant (avec, pour faire plaisir à CinePhil, auto-incrémentation de l'attribut IspId) :
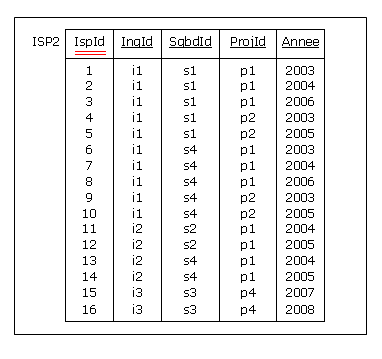
Figure 4.6 - Ajout d'une clé mono-attribut (ISP2)
Les seules dépendances fonctionnelles non triviales vérifiées par ISP2 sont les suivantes :
{IspId} ➔ {IngId},
{IspId} ➔ {SgbdId},
{IspId} ➔ {ProjId},
{IspId} ➔ {Annee},
{IngId, SgbdId, ProjId, Annee} ➔ {IspId}.
Et leurs déterminants respectifs sont les suivants :
{IspId} et {IngId, SgbdId, ProjId, Annee}.
Ces déterminants constituent les seules clés candidates de la table, ce sont donc les seules surclés et
la BCNF est vérifiée (cf. paragraphe 3.3.1). Comme par ailleurs {IspId} est clé mono-attribut,
en vertu du théorème qui vient d'être énoncé, la 4NF est vérifiée elle aussi mais, très mauvaise nouvelle !
les dépendances multivaluées sont piégées ; en effet, si la DMV {IngId} ➔➔ {SgbdId}
vaut pour ISPV et ISP, elle ne vaut plus pour ISP2 qui n'est pas égale à la jointure naturelle de ses projections
{IngId, SgbdId} et {IngId, IspId, ProjId, Annee}. De fait, cette jointure produit des
tuples n'appartenant pas à ISP2 (spurious tuples comme dirait Date) : par exemple, le tuple
<1, i1, s4, p1, 2003> appartient seulement à la jointure.
En revanche, on notera que les DMV {IngId, IspId} ➔➔ {SgbdId}
et {IngId, IspId} ➔➔ {ProjId, Annee} sont vérifiées. En effet, {IspId}
étant clé, toute DF, donc toute DMV dont le multi-déterminant contient IspId est vérifiée (on peut même
invoquer le théorème de Heath puisqu'on peut en rester aux DF). Ainsi ISP2 peut être remplacée par ses
projections {IngId, IspId, SgbdId}
et {IngId, IspId, ProjId, Annee} mais pour un bien piètre résultat, car chacune d'elles
contient autant de tuples qu'ISP2, conséquence de la présence systématique de la clé {IspId} :
on apprend ainsi cinq fois qu'Albert maîtrise IMS et DB2.
On peut dire que si ISP2 et ses projections respectent la 4NF à la lettre, elles la violent dans l'esprit.
Autrement dit, avant d'appliquer la règle « toute clé primaire sera mono-attribut »,
il aurait fallu normaliser
la table ISP et n'appliquer cette règle qu'aux tables Maitriser et Affecter (cf. Figure 4.1)
dont elle est en fait la jointure naturelle ; il y aurait eu cautères sur jambes de bois, mais en tout cas rien
de bien grave puisque, par exemple, il est écrit une fois et une seule qu'Albert maîtrise IMS et DB2.
Les tables Maitriser et Affecter respectent authentiquement la 4NF (et aussi la 6NF, d'ailleurs)
c'est-à-dire non seulement à la lettre, mais aussi dans l'esprit.
4.9. 4NF et relvars « toutes clés », une légende à détruire
Il est de coutume d'affirmer que si le travail de normalisation en BCNF a été mené à son terme,
la vérification de la 4NF ne concerne plus que des relvars dont la clé est composée
de l'ensemble des attributs de leur en-tête.
Il est un fait que jusqu'ici, les relvars et tables que nous avons passées à la moulinette de la 4NF
étaient « toutes clés » : Maitriser, Affecter, ISPV, ISP, ISP2. Mais prenons un exemple
proposé par Chris Date (« What's Normal Anyway? »,
Database Programming & Design, Volume 11 - Number 3, March 1998).
Considérons les règles de gestion de données suivantes, appliquées à une variante de l'exemple classique
des cours dispensés par des enseignants :
(RG1)
Un enseignant enseigne au moins un sujet ;
(RG2)
Un sujet est enseigné par au moins un enseignant ;
(RG3)
Un sujet comporte au moins un thème ;
(RG4)
Un thème fait partie d'au moins un sujet ;
(RG5)
Quel que soit le sujet traité, il n'existe pas de relation particulière entre les enseignants et les thèmes ;
(RG6)
Toutefois, quand un enseignant traite d'un thème, c'est dans le cadre d'un seul sujet.
Ce que veut dire Date avec la règle RG5, c'est que les règles RG2 et RG3 donnent lieu aux dépendances multivaluées :
{Sujet} ➔➔ {Enseignant}
{Sujet} ➔➔ {Theme}
La règle RG6 fait quant à elle l'objet de la dépendance fonctionnelle :
{Enseignant, Theme} ➔ {Sujet}
Un instantané de la relvar SEO correspondante (clé soulignée) :
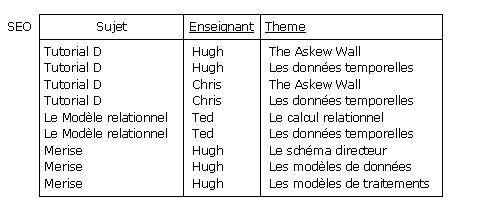
Figure 4.7 - Un instantané de la relvar SEO
La relvar SEO vérifie la BCNF. En effet, elle ne comporte qu'une seule dépendance fonctionnelle non triviale,
à savoir {Enseignant, Theme} ➔ {Sujet} et le déterminant de cette DF est une surclé.
La relvar comporte les dépendances multivaluées non triviales {Sujet} ➔➔ {Enseignant} et
{Sujet} ➔➔ {Theme} mais dont le multi-déterminant {Sujet} n'est pas surclé,
en conséquence de quoi la relvar ne vérifie pas la 4NF.
Il existe donc bien des relvars qui vérifient la BCNF mais pas la 4NF et qui de surcroît sont munies
de clés qui ne se sont pas composées de l'ensemble des attributs de l'en-tête de la relvar.
Afin de normaliser en 4NF, on décompose la relvar SEO par projection (décomposition sans perte de données),
pour obtenir les relvars SE et SO :
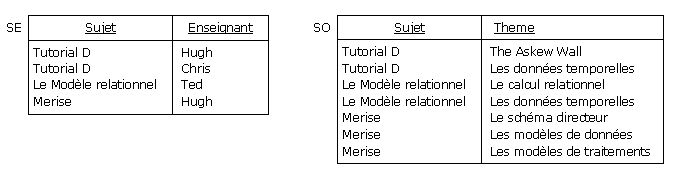
Figure 4.8 - Décomposition de la relvar SEO
Malheureusement on a perdu la DF {Enseignant, Theme} ➔ {Sujet},
c'est-à-dire la règle de gestion RG6. On se retrouve donc face à l'alternative embarrassante,
à savoir normaliser/ne pas normaliser, déjà traitée dans le contexte de la BCNF
(cf. paragraphe 3.7, « Un problème embarrassant de BCNF »).
4.10. La 4NF et Merise
Dans les ouvrages sur Merise, il n'est pas rare de trouver des références à la normalisation.
Ceci est on ne peut plus légitime, puisqu'après tout, les attributs composant l'en-tête d'une relvar ou d'une table,
la liste des propriétés d'une entité-type (voire d'une association-type), la liste des attributs d'une classe,
tout cela peut être vu comme la liste des variables d'un prédicat.
Pour reprendre l'exemple des membres de DVP (cf. Figure 2.4) :
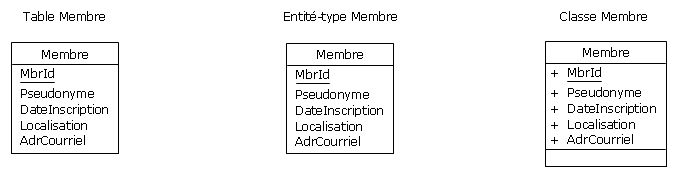
Figure 4.9 - Candidats à faire l'objet de prédicats
Ces représentations correspondent au prédicat pentadique « Membre chez DVP » :
|
Le membre identifié chez DVP par MbrId a pour pseudonyme Pseudonyme, il est inscrit
depuis le DateInscription, il est localisé dans Localisation et il a pour adresse
de courrier électronique AdrCourriel.
|
Étant donné que la normalisation des relvars met en jeu leurs attributs et leurs clés,
il est bien naturel que l'on s'intéresse aussi à la normalisation des entités-types
(et bien sûr des associations-types), en remplaçant les termes
attribut et clé candidate (ou surclé)
par ceux de propriété et d'identifiant, en mettant en évidence les dépendances fonctionnelles
et multivaluées à partir des règles de gestion des données.
Même principe pour les classes mutatis mutandis.
Concernant plus précisément la recherche des viols de 4NF, Fagin a montré
la voie à suivre, mais manifestement celle-ci est escarpée. La recherche des dépendances multivaluées
non triviales dont les parties gauches ne sont pas des surclés est un exercice qui pour sa part n'est pas
toujours ... trivial.
En ce sens, considérons à nouveau la table SQL ISP2 (cf. Figure 4.6). Le diagramme dans lequel elle s'intègre
est le suivant (les attributs composant la clé alternative {IngId, SgbdId, ProjId, Annee}
sont soulignés en pointillés, et ceux qui participent aux clés étrangères sont en italiques) :
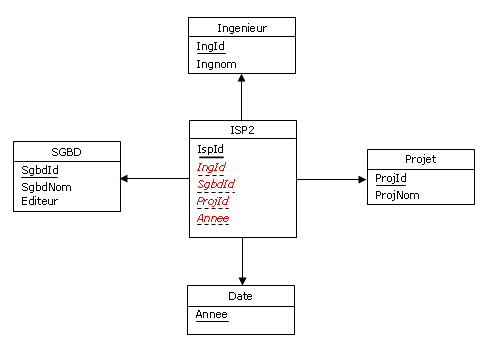
Figure 4.10 - Table ISP2 avant rétroconception
Si l'on effectue une rétroconception orientée Merise, on obtient la représentation conceptuelle suivante
(dans laquelle on a renommé ISP2 en CV, comme Curriculum Vitae) :
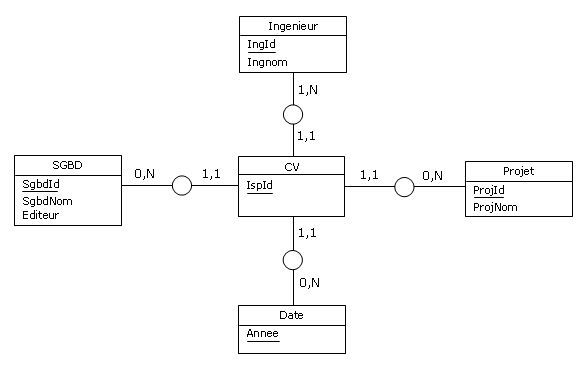
Figure 4.11 - Rétroconception de la table ISP2
A moins de se poser des questions sur l'absence de propriétés naturelles concernant l'entité-type CV
et sur l'absence des associations-types telles que Maitriser et Affecter, il est probable qu'on ne
cherchera malheureusement pas à débusquer un viol de 4NF pour cette entité-type peccamineuse.
Dans le même sens, considérons à nouveau la relvar ISP (cf. paragraphe 4.7). Le diagramme dans lequel
elle s'intègre est le suivant :
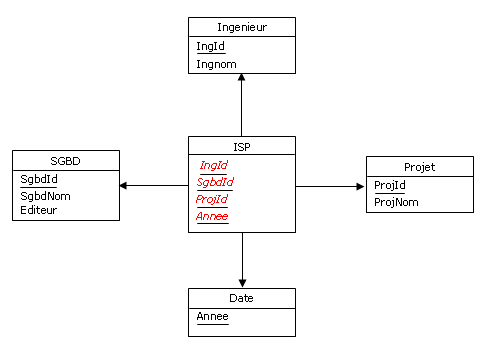
Figure 4.12 - Relvar ISP avant rétroconception
Par rétroconception on obtient la représentation conceptuelle suivante
(dans laquelle on a renommé ISP en ConstituerCV) :
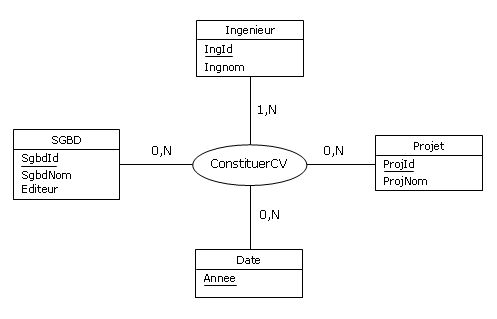
Figure 4.13 - Rétroconception de la relvar ISP
Le merisien averti, habitué à expertiser les associations-types de dimension supérieure à deux, confrontera
cette représentation aux règles de gestion de données. De deux choses l'une :
 |
Ou bien ces règles précisent qu'effectivement on doit connaître les SGBD utilisés par les ingénieurs dans le
cadre des projets, auquel cas le prédicat suivant est le bon (cf. « Piège de la connexion »
au paragraphe 4.2) :
(P3)
Hxyzw : L'ingénieur IngId a utilisé le SGBD SgbdId dans le
cadre du projet ProjId au cours de l'année Annee
Mais en conséquence de quoi le MCD doit résulter de la rétroconception du MLD de la Figure 4.4 :
|
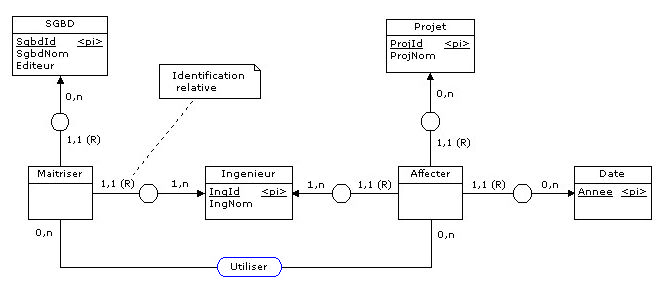
Figure 4.14 - Utilisation des SGBD par les ingénieurs dans le cadre des projets
 |
Ou bien ces règles ne précisent rien en ce sens et ce sont seulement celles qui ont été énoncées
au paragraphe 4.2 qui prévalent (RG1 et RG3), auquel cas la représentation de la Figure 4.13 doit être
remplacée par la suivante, radicalement différente et
conforme aux prédicats P1 et P2 (paragraphe 4.2) :
|
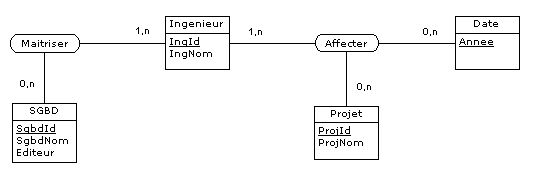
Figure 4.15 - Compétences et affectations des ingénieurs
Autrement dit, si l'on interprète correctement les règles de gestion des données et si l'on procède à
ce remplacement, alors on montre que l'on sait modéliser, sans nécessairement connaître la 4NF.
Néanmoins, maîtriser le concept de dépendance
multivaluée et savoir débusquer les viols de 4NF est préférable si l'on veut être sûr de ne rien laisser passer.
L'exemple du paragraphe 4.11, extrait d'un cas réel, est là pour montrer que l'on peut avoir des distractions
qui pourraient coûter cher.
4.11. Merise et la chasse aux ternaires
On peut conjecturer que les viols de 4NF sont rares, mais il n'en demeure pas moins que lorsqu'ils se
produisent, ils ne sautent pas aux yeux. Si on veut les débusquer, il faut, en amont, auditer les
associations-types ternaires (et au-delà), qui figurent dans les diagrammes conceptuels.
Dans les années quatre-vingts, j'ai eu à expertiser le MCD (modèle conceptuel de données) d'une
application bancaire ayant pour titre : « Déclaration des risques à la Banque de France ».
Remontons dans le passé... Les établissements bancaires français sont donc tenus de faire des
déclarations périodiques quant à l'état des crédits qu'ils consentent à leurs clients. Pour sa part,
la Banque de France a pour mission de rassembler l'ensemble des déclarations effectuées par les
établissements bancaires, et en retour, d'envoyer à chacun d'eux les récapitulatifs des risques
au niveau national pour chaque client.
La banque dont j'expertise le MCD est la B.R.L. (Banque du Relationland, bien sûr...) Cette banque est organisée
en guichets et filiales. L'objet de la déclaration est de fournir la liste des clients et de leurs
contrats quand les sommes engagées dépassent un certain seuil, ainsi que la liste des établissements
déclarants (guichets et filiales de la banque) garantissant les engagements.
Le fragment qui nous intéresse de la structure prévue dans le Système d'Information est le suivant :
les contrats, les clients et les déclarants (constitués en pools pour gérer et garantir les contrats).
La partie correspondante du MCD est la suivante, d'allure tout à fait honnête, bien sûr noyée dans un
diagramme d'une cinquantaine d'entités-types et d'associations-types, mais on arrive à y repérer
l'association-type ternaire suivante :
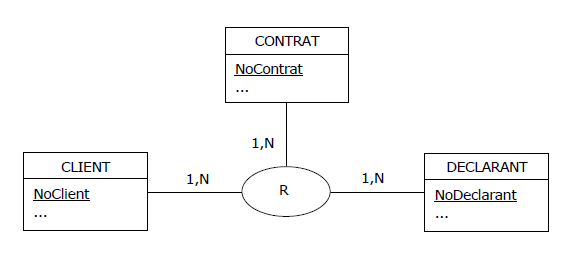
Figure 4.16 - MCD - Déclaration des risques
Une ternaire ? Suspicion ! Après entretien avec le chef de projet, les règles de gestion
intéressantes se résumaient à celles-ci :
(R1) Un client est titulaire d'au moins un contrat ;
(R2) Un contrat a au moins un client pour titulaire ;
(R3) Un déclarant garantit au moins un contrat ;
(R4) Un contrat est garanti par au moins un déclarant.
Mais pas la moindre règle faisant état de relations entre les déclarants et les clients ; celles-ci
existaient bien entendu, mais ne jouaient aucun rôle dans le cadre des déclarations des risques :
pour chaque contrat faisant l'objet d'une déclaration, les clients co-titulaires du contrat étaient
indépendants des déclarants garants du contrat. Autrement dit, l'association-type R
(Déclarer contrat, de son vrai nom) aurait donné lieu à une table SQL violant la 4NF,
du fait qu'elle aurait comporté les dépendances multivaluées non élémentaires suivantes :
{NoContrat} ➔➔ {NoClient}
{NoContrat} ➔➔ {NoDeclarant}
Pour éviter une telle situation délinquante et fort périlleuse pour l'application, une seule solution :
en s'appuyant sur le 1er théorème de Fagin, « casser » R et produire le MCD suivant,
avec R = R1 JOIN R2 :
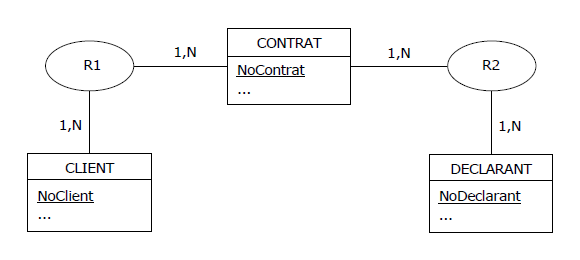
Figure 4.17 - MCD - Déclaration des risques - Respect de la 4NF
Sitôt dit, sitôt fait.
L'exemple présenté se veut didactique. En réalité, contexte bancaire oblige,
tout est daté, y compris les déclarations de risques. Autrement dit, le MCD initial
tient compte des périodes couvertes par les déclarations :
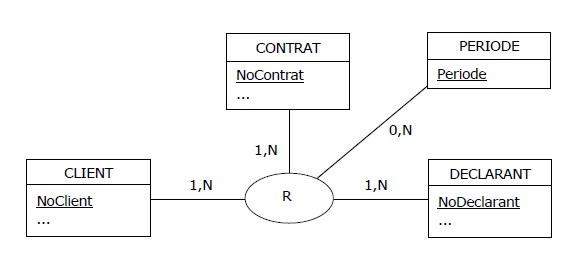
Figure 4.18 - MCD - Déclarations datées, avant normalisation
Après normalisation :
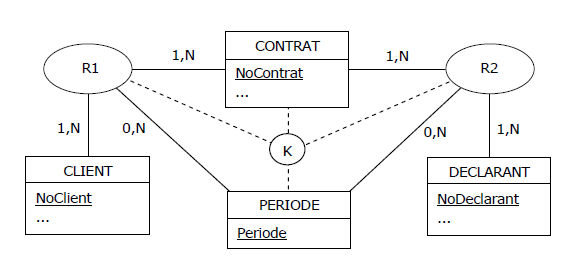
Figure 4.19 - MCD - Déclarations datées, après normalisation
 |
K représente graphiquement la contrainte suivante :
R1 {NoContrat, Periode} = R2 {NoContrat, Periode}
A savoir qu'au niveau relationnel, les projections de R1 et de R2 sur les attributs NoContrat et Periode
doivent être égales. La contrainte K est garantie de facto avant normalisation, mais sans sa présence
après normalisation, qu'est-ce qui empêcherait que pour un contrat donné on ait des périodes différentes
côté CLIENT et côté DECLARANT ?
|
4.12. Observations concernant la décomposition des relvars
Les relvars Maitriser et Affecter présentées au paragraphe 4.2 respectent la 4NF, contrairement aux
relvars ISPV (paragraphe 4.2) et ISP (paragraphe 4.7). De même, les relvars issues des associations-types
R1 et R2 (paragraphe 4.11) sont en 4NF elles aussi, contrairement à la relvar R. Dans la mesure où l'on a
fait du préventif (
better prevent than cure comme dit un de mes amis qui vit au Relationland), tout est
pour le mieux dans le meilleur des mondes. J'ai écrit au paragraphe 4.7 que la relvar ISP violait la 4NF,
mais qu'elle était décomposable selon Maitriser et Affecter,
so far so good.
Modifions maintenant légèrement
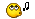
les règles de gestion RG1 et RG3
énoncées au paragraphe 4.2.
Règles initiales :
(RG1) Un ingénieur est compétent pour au moins un SGBD.
(RG3) Un ingénieur a été affecté à au moins un projet.
Nouvelles règles :
(RG1') Un ingénieur peut être compétent pour au moins un SGBD.
(RG3') Un ingénieur a pu être affecté à au moins un projet.
Cette fois-ci, il se peut que des ingénieurs n'aient pas de compétences en termes de SGBD (Philou et Mimile)
ou qu'ils n'aient pas été affectés à des projets (Denis et Mimile).
Un instantané :
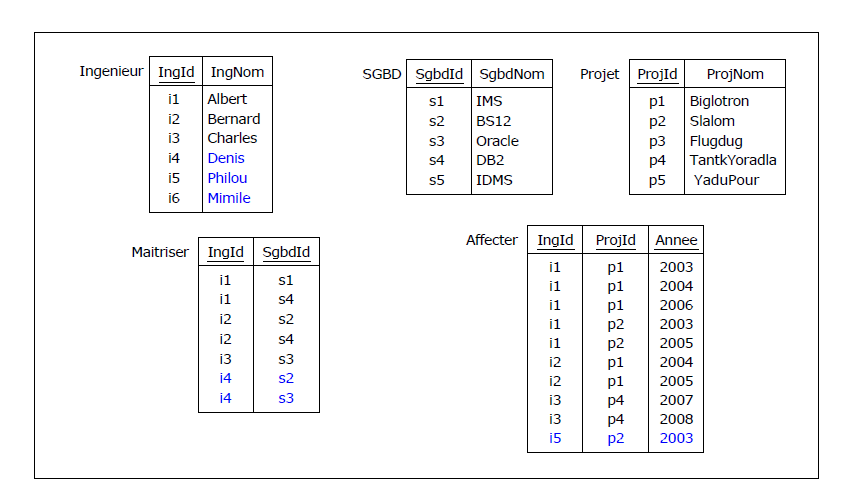
Figure 4.20 - Les ingénieurs, leurs SGBD, leurs projets (nouvel instantané)
La vue ISPV, jointure naturelle des relvars Affecter et Maitriser ne change pas de valeur par comparaison
avec celle qu'elle avait quand Denis, Philou et Mimile ne figuraient pas dans les effectifs :
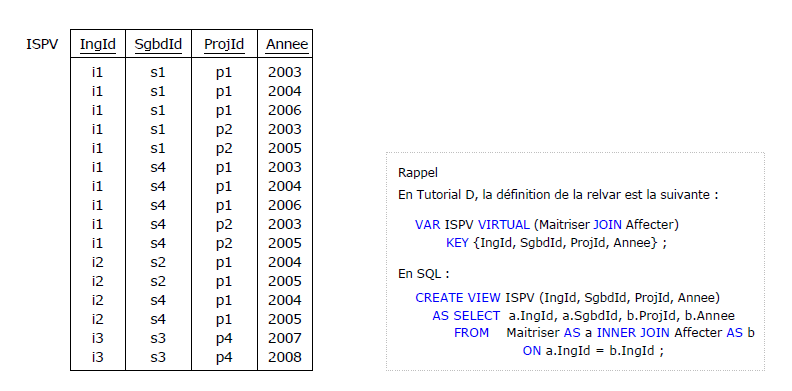
Figure 4.21 - ISPV : Jointure naturelle des tables Maitriser et Affecter
En effet, il faut se souvenir que le prédicat d'ISPV est dérivé, qu'il est la conjonction des prédicats
P1 et P2 (cf. paragraphe 4.2), c'est-à-dire qu'ISPV ne permet de voir (a) que les ingénieurs
qui maîtrisent au moins un SGBD et (b) qui ont été affectés à au moins un projet. Si l'on applique le
1er théorème de Fagin, on produira deux vues, disons ISPV1 et ISPV2 qui ne permettront de manipuler
que des sous-ensembles a priori stricts des relvars Maitriser et Affecter (Denis et Philou en sont exclus),
leur intérêt est donc nul.
Supposons maintenant que nous ayons mis en oeuvre la relvar de base ISP évoquée au paragraphe 4.7, censée
remplacer Maitriser et Affecter : au niveau logique, on ne disposera que du diagramme de la Figure 4.12 et
au niveau conceptuel que de celui de la Figure 4.13.
Mais cette fois-ci, il va falloir impérativement prendre en compte les ingénieurs qui, à l'image de Denis et
Philou n'ont pas forcément de compétences en SGBD ou n'ont pas été affectés à des projets. Du coup, ISP se met
à ressembler à n'importe quoi, avec l'apparition de valeurs « spéciales », du genre chaîne vide
comme ci-dessous (ou pire encore, celle du bonhomme NULL) :
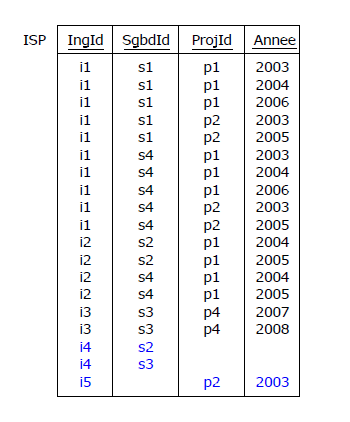
Figure 4.22 - Relvar ISP, supposée remplacer à la fois Maitriser et Affecter
Mais là encore, il est évident que la projection d'ISP sur {IngId, SgbdId} d'une part et
{IngId, ProjId, Annee} d'autre part ne permettra pas de reproduire les relvars Maitriser
et Affecter, mais produira les relvars polluées, ISPa et ISPb :
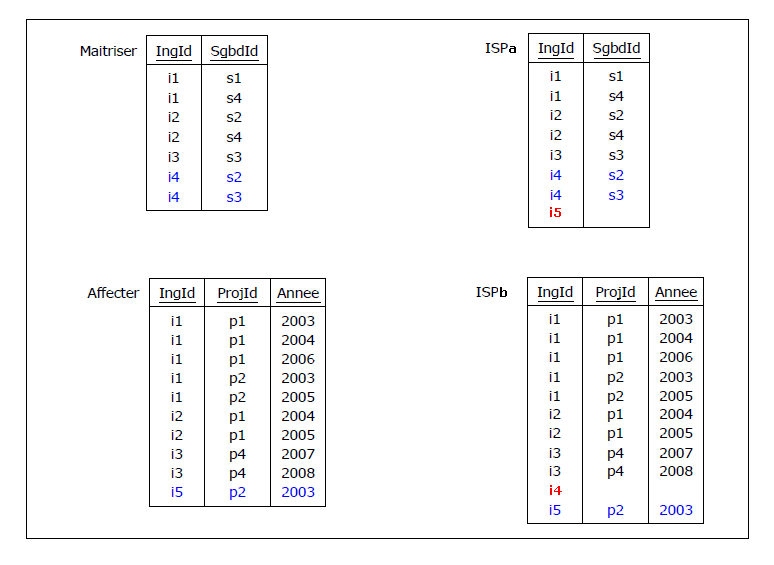
Figure 4.23 - Relvars ISPa et ISPb, supposées remplacer Maitriser et Affecter
La situation devient cauchemardesque si les partisans du bonhomme du NULL se mettent de la partie, car ISP
(devenue table), ne peut même plus être dotée d'une clé primaire :
.png)
Figure 4.24 - Table ISP infectée
Mais évidemment, les sectateurs du bonhomme du NULL bricoleront une rustine en définissant une colonne ad-hoc,
IspId, comme dans le cas de la table ISP2 (cf. paragraphe 4.8) qui aurait alors pour clé primaire {IspId}
(auto-incrémentée pour faire bonne mesure) et pour contenu
(dans le moins pire des cas, c'est-à-dire si les dépendances multivaluées sont respectées) :
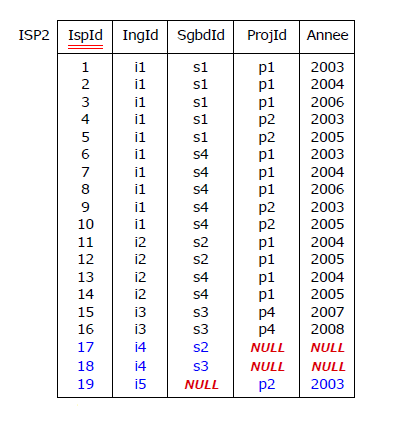
Figure 4.25 - Ajout d'une clé primaire ad-hoc (table ISP2)
On n'ose imaginer les conséquences d'une telle approche sur l'application
« Déclaration des risques à la Banque de France » (cf. paragraphe 4.11)... Une fois de plus,
mieux vaut prévenir que guérir et s'assurer au plus tôt du respect de la 4NF.
4.13. Approche ascendante vs approche descendante
Les auteurs spécialistes de Merise ne traitent pas de la 4NF à la manière dont nous l'avons fait ici.
Tout au plus certains se bornent à la nommer, tandis que d'autres la connaissent très bien mais, sans
y faire explicitement référence, usent de circonlocutions pour résoudre les viols de 4NF.
A ce sujet, voir par exemple [Tabourier 1986] au paragraphe 6.2.5 « Problématique de la
décomposition/normalisation », à propos de l'exercice fameux traitant des personnes qui conduisent
des voitures et pénètrent dans des bâtiments.
En l'occurrence, Tabourier ne donne aucune définition de la dépendance multivaluée et de la 4NF,
il n'énonce aucun théorème, mais il connaît très bien le sujet, il manœuvre à la perfection et
explique les bienfaits de la décomposition des associations-types impliquées dans cette affaire. Chapeau !
Mais à cette occasion (cf. pages 96-97 de son ouvrage), Tabourier s'en prend de façon surprenante aux spécialistes
du Modèle Relationnel de Données
(en l'occurrence Zaniolo, dont il cite l'article, à savoir [Zaniolo 1981]),
à propos de l'élaboration de la structure des relvars :
 |
« [Des] propositions très en vogue dans l´approche relationnelle suggèrent de mettre au jour les
dépendances entre les informations élémentaires, puis d'appliquer des techniques algorithmiques ou
interactives pour rassembler ces informations par
 paquets paquets et construire ainsi la structure du
modèle [...] Même en se limitant aux informations dûment répertoriées antérieurement,
on dispose souvent de quelques milliers d'informations élémentaires, donc de quelques millions de
couples d'informations, ce qui ne représente qu'une partie des dépendances possibles : bon courage ! »
et construire ainsi la structure du
modèle [...] Même en se limitant aux informations dûment répertoriées antérieurement,
on dispose souvent de quelques milliers d'informations élémentaires, donc de quelques millions de
couples d'informations, ce qui ne représente qu'une partie des dépendances possibles : bon courage ! »
|
Et plus loin (cf. page 169 du même ouvrage) :
 |
« Le relationnel se présente, dans son esprit, comme une pure structure de données. Une obsession
des chercheurs consiste d'ailleurs dans la question suivante : comment construire un ensemble minimal
(en un certain sens) de schémas relationnels, rendant compte des dépendances de diverses natures
( fonctionnelles fonctionnelles , ,
 multivaluées multivaluées , ,
 de jointure de jointure ) entre les constituants d'un
vaste schéma unique ( ) entre les constituants d'un
vaste schéma unique (
 universel universel ) initial ? » ) initial ? »
|
Halte au feu ! Le Modèle Relationnel ne se présente pas comme le prétend Tabourier. Je cite Ted Codd ([Codd 1980]) :
 |
« Numerous authors appear to think of a data model as nothing more than a collection of data structure types.
This is like trying to understand the way the human body functions by studying anatomy but omitting physiology.
The operators and integrity rules are essential to any understanding of how the structures behave. In comparing
data models people often ignore the operators and integrity rules altogether. When this occurs, the resulting
comparisons run the risk of being meaningless. »
(Il apparaît que de nombreux auteurs pensent qu'un modèle de données n'est rien de plus qu'une collection de types
de structures de données. C'est comme si on essayait de comprendre le fonctionnement du corps humain par l'étude
de l'anatomie mais sans tenir compte de la physiologie. Les opérateurs et les règles d'intégrité sont essentiels
pour comprendre comment se comportent les structures. En comparant les modèles de données, les gens ignorent
souvent les opérateurs et les règles d'intégrité. Quand il en est ainsi, les comparaisons courent le risque
d'être dénuées de sens.)
|
C'est de façon évidemment très formelle que pour sa part Zaniolo décrit les concepts et les algorithmes
permettant de normaliser sans erreur et omission : tout au plus doit-on reconnaître qu'il faut
s'accrocher pour apprécier son article de 50 pages à lire très, très, très lentement.
A titre indicatif, voici la définition que Zaniolo donne de la dépendance multivaluée :
|
« Si Θ et Δ sont des combinaisons d'attributs de la relation R(Ω), et r ∈ R, alors
l'ensemble des Δ-valeurs associées à la valeur r[Θ] est notée MΔ(r[Θ]).
On peut formellement écrire :
|
MΔ(r[Θ]) = {r′ [Δ] | r′ ∈ R
et r′ [Θ] = r[Θ]}
Ou un aperçu de ses considérations sur un certain algorithme de décomposition :
« [...] Ainsi l'algorithme 5.1 a une limite supérieure évidente égale à
O (n4 log n) où n représente la cardinalité de
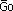  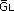 .
Cependant, la limite polynomiale ne s'applique qu'une fois
calculés .
Cependant, la limite polynomiale ne s'applique qu'une fois
calculés 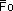 , ,
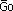 et et 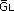 ,
puisque la taille de ces ensembles peut
être exponentielle [...] » ,
puisque la taille de ces ensembles peut
être exponentielle [...] »
|
A sa façon, Zaniolo nous souhaite lui aussi « Bon courage ! »
Disons que l'approche de Tabourier est descendante, tandis que celle de Zaniolo est ascendante,
et la relation universelle à laquelle Tabourier fait allusion ne concerne pas
les praticiens que nous sommes, astreints à produire des résultats selon un calendrier serré.
Autrement dit, procédons d'abord comme Tabourier, commençons par produire des modèles conceptuels de données
avec les entités-types et associations-types comportant les propriétés pertinentes.
Mais n'en restons pas là, sortons ensuite l'artillerie lourde et, entité-type par entité-type,
association-type par association-type, assurons-nous que la 4NF est respectée, grâce aux théorèmes,
algorithmes et tous outils fournis par Codd, Fagin, Zaniolo et compagnie.
Comme disait Poincaré à peu près en ces termes :
« L'intuition trouve, le raisonnement prouve ».
Incidemment, si Tabourier s'en prend aux spécialistes du Modèle Relationnel de Données, on peut faire observer
que certains spécialistes de la méthode Merise préconisent eux aussi de commencer par fournir
— à partir d'un inventaire baptisé dictionnaire des données —
un graphe des
dépendances fonctionnelles, une structure d'accès théorique (sic !) ou couverture minimale
(un ersatz en fait de la couverture irréductible étudiée au paragraphe E.6),
ainsi qu'une matrice de ces dépendances pour en déduire les entités-types et
associations-types des modèles conceptuels de données (quant à elles, les dépendances multivaluées
et de jointure font l'objet d'un silence « éloquent »...)
Voir par exemple [Matheron 2002].
Quoi qu'il en soit, pour reprendre les termes de Tabourier,
avec des milliers d'informations élémentaires (n'oubliez pas O (n4 log n)...),
alors d'accord : « Bon courage ! »
Pour conclure avec Merise à propos de la normalisation :
Quand on en a bien compris l'enjeu et qu'on a eu à la pratiquer sans se relâcher,
on ne peut rester indifférent à ce qui suit :
« La normalisation des tables consiste à répartir les informations dans les tables en fonction de règles.
Seules les clés peuvent être redondées. Cinq étapes de normalisation sont distinguées. A chaque étape,
les tables sont déclarées comme étant en première, deuxième... cinquième forme normale. Le but est
d'arriver à la dernière étape pour obtenir des tables normalisées.
Cette normalisation est obligatoire uniquement si les tables ont été directement construites sans méthode.
Ces règles peuvent être rapprochées des règles sur les informations d'individus ou de relation
(une seule valeur d'information par individu ou relation par exemple).
Quand le passage s'effectue du MCD MOD (MLD) au MPD, les tables sont obligatoirement normalisées.
Merise évite d'avoir à normaliser les tables. »
|
Aux innocents les mains pleines...
L'auteur de ces lignes — qui n'est d'ailleurs pas le seul à tenir ce genre de propos —
est Michel Diviné qui a eu l'élégance de mettre à la disposition de tous son
ouvrage « Parlez-vous Merise » (cf. [Diviné 1989]). Diviné est très bon dans sa partie,
c'est-à-dire Merise, mais quand il en arrive au stade relationnel, ses considérations et
conclusions relèvent de l'incantation et sont bonnes pour le pilon
(voyez le chapitre qu'il a consacré au MPD). Qu'il nous pardonne ce jugement plutôt sévère,
mais Merise n'évite pas d'avoir à normaliser, pas plus que la peur n'évite le danger,
même s'il faut reconnaître que violer la 4NF n'est sans doute pas courant (conjecturons-le)
quand on sait bâtir un MCD Merise ou un diagramme de classes UML et que l'on sait normaliser en BCNF.
4.14. Implication de la BCNF par la 4NF
A titre de récréation et pour réfuter les conclusions hallucinantes du clerc qui met en cause Delobel et Adiba
(cf. paragraphe 2.8), nous reprenons ici la démonstration de l'implication de la BCNF par la 4NF,
telle qu'elle figure dans [Delobel 1982]. D. & A. remplacent le terme BCNF par celui
de 3FNBCK, en l'honneur de William Kent qui a aiguillé les recherches de Boyce et Codd, ses
collègues chez IBM. De même ils écrivent « 4FN », plus conforme en français que « 4NF ».
L'expression « Schéma R » (R souligné) est à prendre ici comme synonyme de « relvar ».
Voici la démonstration donnée dans [Delobel 1982], dans laquelle X ➔ Y représente une
DF non triviale :
 |
« On peut noter que la 4FN implique la 3FNBCK. En effet, supposons qu'un schéma R
soit en 4FN et pas en 3FNBCK. D'après la définition de la 3FNBCK, il existe une
dépendance X ➔ Y où X ne contient pas une clé. Si X ➔ Y
est vérifiée dans R, la dépendance multivaluée X ➔➔ Y
l'est aussi. Or puisque R est en 4FN, X doit contenir une clé, d'où la
contradiction. »
|
De fait, par référence à la définition de la BCNF (cf. paragraphe 3.3.1), si X et Y sont des
sous-ensembles d'attributs de R, alors R est en BCNF si et seulement si pour
chaque DF non triviale X ➔ Y qui doit être vérifiée, le déterminant X
de cette DF est une surclé de R. Si donc R n'est pas en BCNF, a contrario
il existe une DF non triviale X ➔ Y dont le déterminant X n'est pas surclé.
Mais d'après la règle de réplication (cf. paragraphe 4.5), si X ➔ Y
alors X ➔➔ Y : le multi-déterminant X de cette DMV n'étant pas surclé,
R n'est donc pas en 4NF, en contradiction avec l'hypothèse de départ.
On trouve dans [Korth 1986] exactement la démonstration de Delobel et Adiba. On trouvera d'autres
démonstrations de cette preuve notamment dans [Fagin 1977] : Theorem 2, ou dans
[Maier 1983] : Chapter 7, Lemma 7.2.


Copyright © 2008 - François de Sainte Marie.
Aucune reproduction, même partielle, ne peut être faite
de ce site ni de l'ensemble de son contenu : textes, documents, images, etc.
sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à
trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.








.jpg) DMV1 : {IngId} ➔➔ {SgbdId}
Ce qui se lit : {SgbdId} est multi-dépendant de {IngId}, ou encore
{IngId} multi-détermine {SgbdId} ;
DMV1 : {IngId} ➔➔ {SgbdId}
Ce qui se lit : {SgbdId} est multi-dépendant de {IngId}, ou encore
{IngId} multi-détermine {SgbdId} ;
.jpg) DMV2 : {IngId} ➔➔ {ProjId, Annee}
{ProjId, Annee} est multi-dépendant de {IngId},
{IngId} multi-détermine {ProjId, Annee}.
DMV2 : {IngId} ➔➔ {ProjId, Annee}
{ProjId, Annee} est multi-dépendant de {IngId},
{IngId} multi-détermine {ProjId, Annee}.



 ,
z
,
z >
deux tuples appartenant à R, la dépendance multivaluée
X ➔➔ Y est vérifiée si et seulement si les tuples
<x,
y
>
deux tuples appartenant à R, la dépendance multivaluée
X ➔➔ Y est vérifiée si et seulement si les tuples
<x,
y ,
z> et <x, y,
z
,
z> et <x, y,
z >
appartiennent aussi à R.
>
appartiennent aussi à R.
 ,
z
,
z >
de R, on a y = y
>
de R, on a y = y . Il s'ensuit que
la condition d'existence des tuples <x,
y
. Il s'ensuit que
la condition d'existence des tuples <x,
y ,
z> et <x, y,
z
,
z> et <x, y,
z > est
de facto vérifiée,
en vertu de quoi la dépendance multivaluée X ➔➔ Y est vérifiée elle aussi,
ce qui donne lieu à la règle dite de réplication :
> est
de facto vérifiée,
en vertu de quoi la dépendance multivaluée X ➔➔ Y est vérifiée elle aussi,
ce qui donne lieu à la règle dite de réplication :



.jpg) √ Cette dépendance multivaluée est triviale.
√ Cette dépendance multivaluée est triviale.
.jpg) √ La dépendance fonctionnelle X ➔ {A} est vérifiée pour chaque
attribut A de H (X est alors une surclé de R).
√ La dépendance fonctionnelle X ➔ {A} est vérifiée pour chaque
attribut A de H (X est alors une surclé de R).
.jpg) DMV1 : {IngId} ➔➔ {SgbdId}
DMV1 : {IngId} ➔➔ {SgbdId}
.jpg) DMV2 : {IngId} ➔➔ {ProjId, Annee}
DMV2 : {IngId} ➔➔ {ProjId, Annee}
non_indente.jpg)
 R2) ➔➔ (R1 — R2)
ou (R1
R2) ➔➔ (R1 — R2)
ou (R1  R2) ➔➔ (R2 — R1).
R2) ➔➔ (R2 — R1).
 R2 est égal à {IngId} et R1 — R2
est égal à {SgbdId}. Comme la DMV {IngId} ➔➔ {SgbdId} est donnée, on vérifie bien
(R1
R2 est égal à {IngId} et R1 — R2
est égal à {SgbdId}. Comme la DMV {IngId} ➔➔ {SgbdId} est donnée, on vérifie bien
(R1  R2) ➔➔ R1 — R2,
donc la relvar ISP est décomposable sans perte de données, et l'on retrouve ainsi les relvars Maitriser
et Affecter (cf. figure 4.2).
R2) ➔➔ R1 — R2,
donc la relvar ISP est décomposable sans perte de données, et l'on retrouve ainsi les relvars Maitriser
et Affecter (cf. figure 4.2).
.jpg) DMV1 : {IngId} ➔➔ {ProjId} | {Annee}
DMV1 : {IngId} ➔➔ {ProjId} | {Annee}
.jpg) DMV2 : {ProjId} ➔➔ {IngId} | {Annee}
DMV2 : {ProjId} ➔➔ {IngId} | {Annee}
.jpg) DMV3 : {Annee} ➔➔ {IngId} | {ProjId}
DMV3 : {Annee} ➔➔ {IngId} | {ProjId}















 les règles de gestion RG1 et RG3
énoncées au paragraphe 4.2.
les règles de gestion RG1 et RG3
énoncées au paragraphe 4.2.




.png)


 paquets
paquets et construire ainsi la structure du
modèle [...] Même en se limitant aux informations dûment répertoriées antérieurement,
on dispose souvent de quelques milliers d'informations élémentaires, donc de quelques millions de
couples d'informations, ce qui ne représente qu'une partie des dépendances possibles : bon courage ! »
et construire ainsi la structure du
modèle [...] Même en se limitant aux informations dûment répertoriées antérieurement,
on dispose souvent de quelques milliers d'informations élémentaires, donc de quelques millions de
couples d'informations, ce qui ne représente qu'une partie des dépendances possibles : bon courage ! »

 fonctionnelles
fonctionnelles ,
,
 multivaluées
multivaluées ,
,
 de jointure
de jointure ) entre les constituants d'un
vaste schéma unique (
) entre les constituants d'un
vaste schéma unique (
 universel
universel ) initial ? »
) initial ? »


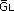 .
Cependant, la limite polynomiale ne s'applique qu'une fois
calculés
.
Cependant, la limite polynomiale ne s'applique qu'une fois
calculés 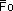 ,
,
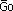 et
et 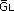 ,
puisque la taille de ces ensembles peut
être exponentielle [...] »
,
puisque la taille de ces ensembles peut
être exponentielle [...] »
