Bases de données relationnelles et normalisation :
de la première à la sixième forme normale
Date de publication : 07/09/2008. Date de mise à jour : 14/07/2012.
5. Cinquième forme normale
5.1. Introduction
5.2. Dépendance de jointure
5.3. Relvars formant un cycle
5.4. Dépendance de jointure triviale
5.5. Définition de la 5NF (PJ/NF)
5.6. Exemples de relvars respectant ou non la 5NF
5.7. Parallèle entre la BCNF, la 4NF et la 5NF
5.8. Un autre théorème de Date et Fagin
5.9. Pour conclure avec la normalisation en 5NF
5.10. Un petit exercice
5. Cinquième forme normale
5.1. Introduction
Résumons ce que nous savons jusqu'ici de la normalisation. D'un point de vue technique, la normalisation en 2NF,
3NF, BCNF consiste à décomposer par projection une relvar non normalisée, en appliquant le théorème de Heath
(cf. paragraphe 3.3.2) — ou une de ses variantes (cf. paragraphe E.7.1) —, théorème qui met en jeu
les dépendances fonctionnelles :
|
Soit la relvar R {A, B, C} dans laquelle A, B et C sont des sous-ensembles d'attributs. Si R satisfait
à la dépendance fonctionnelle A ➔ B, alors R est égale à la jointure de ses projections
sur {A, B} et {A, C}.
|
Même principe quand il s'agit de la normalisation en 4NF qui consiste à décomposer par projection une relvar non
normalisée, en appliquant le premier théorème de Fagin (cf. paragraphe 4.4), lequel met en jeu les
dépendances multivaluées (en notant le « si et seulement si »
caractérisant la préservation des dépendances multivaluées) :
|
Soit la relvar R {A, B, C} dans laquelle A, B et C sont des ensembles d'attributs.
R est égale à la jointure de ses projections sur {A, B} et {A, C} si et seulement si
R vérifie les dépendances multivaluées
A ➔➔ B et A ➔➔ C.
|
L'application de ces théorèmes consiste à décomposer par projection une relvar R non normalisée
en
deux relvars R1 et R2 dont la jointure naturelle est égale à R (décomposition sans perte de données),
étant entendu que la normalité de R1 et R2 est à vérifier à son tour.
Au bout du compte, chaque relvar de la base de données doit respecter la 4NF,
au moins en théorie, car certaines situations (rares il est vrai) peuvent être embarrassantes
(cf. paragraphes 3.7 et 4.9).
Mais on peut aller plus loin. Dans son tout premier article ([Codd 1969], pages 7 et suivantes),
Codd nota déjà que certaines relvars ne pouvaient pas être décomposées sans perte de données en deux
projections, mais pouvaient l'être par décomposition en
trois projections (ou plus)
formant un cycle (cf. "
cyclic 3-joins" dans l'article). Comme l'écrit Chris Date («
The Birth of the Relational Model - Part 2 ») :
|
Remarkably, Codd also gives an example that shows he was aware back in 1969 of the fact that some
relations can't be nonloss-decomposed into two projections but can be nonloss-decomposed into three!
This example was apparently overlooked by most of the paper's original readers; at any rate, it
seemed to come as a surprise to the research community when that same fact was rediscovered several
years later...
|
Quoi qu'il en soit, huit ans plus tard, Aho, Beeri et Ullman étudièrent de très près cette affaire,
suivis par Jorma Rissanen et Jean-Marie Nicolas. Des travaux de ces chercheurs résulta le concept de
dépendance de jointure (DJ ou JD pour join dependency),
sorte de troisième étage de la fusée, bien calé sur les DF et les DMV. Les propriétés des DJ furent
minutieusement étudiées et motivèrent à son tour Fagin qui nous livra son très bel article de 1979
« Normal forms and relational database operators » (cf. [Fagin 1979]).
C'est à lui que revint l'honneur de découvrir la 5NF (qu'il préféra appeler Project/Join Normal Form (PJ/NF),
« 5NF » manquant un peu de sel, d'autant plus qu'il montra qu'avec la décomposition des relvars
par le mécanisme de projection/jointure, on ne pouvait aller plus loin). Dans ce qui suit,
quand nous mentionnons Fagin sans précision particulière, nous faisons implicitement référence à cet article.
Le sujet de la normalisation par projection/jointure était clos (à ceci près qu'une vingtaine d'années plus tard
Date proposa une 6e forme normale,
car certaines relvars en 5NF peuvent encore être décomposées avec grand profit, quand des données de type intervalle
— essentiellement temporelles — sont parties prenantes).
En tout état de cause, Aho et les autres montrèrent que certaines relvars comportent des redondances face
auxquelles les dépendances fonctionnelles et les dépendances multivaluées ne nous sont d'aucun secours, mais qui ne
résistent pas à une attaque par les dépendances de jointure, la 5NF étant là pour nous assurer d'une base
de données bien normalisée.
5.2. Dépendance de jointure
Définition :
Les sous-ensembles X1, X2, ..., Xn sont encore appelés les composants de la DJ.
En particulier, si son en-tête ne comporte que deux sous-ensembles d'attributs, disons A et B, la relvar
R {A, B} vérifie la DJ ★{A, B} si et seulement si elle est égale à la jointure de ses
projections sur A et B.
Faisant référence à son 1er théorème (cf. paragraphe 4.4), Fagin précise que toute dépendance multivaluée peut être
représentée par une dépendance de jointure. Soit la relvar R {A, B, C} où A, B, C sont des
sous-ensembles d'attributs de R, l'union de A et de B étant notée AB et celle de A et de C notée AC :
|
La dépendance multivaluée A ➔➔ B est vérifiée par R si et seulement si
la dépendance de jointure ★{AB, AC} l'est aussi.
|
Ce que Date résume ainsi de façon synthétique :
A ➔➔ B | C Ξ ★{AB, AC}
Ainsi, la dépendance multivaluée est un cas particulier de la dépendance de jointure, mais il y a des DJ qui ne
sont pas des DMV et qu'on cherchera à mettre en évidence, en partant du principe qu'elles comportent
alors plus de deux composants.
5.3. Relvars formant un cycle
Considérons le diagramme merisien ci-dessous, selon lequel les ingénieurs spécialistes en
bases de données de la SARL Les Prévoyants de l'Avenir des Bases de Données (LPABDD, filiale de DVP),
sont affectés chez les clients de cette entreprise, afin d'administrer les bases de données de ces derniers,
les piloter dans l'utilisation des SGBD, etc.
Au sens du père du modèle relationnel de données, on est en présence d'un cycle
(cf. "cyclic 3-join" dans [Codd 1969]) :
.png)
Figure 5.1 - MCD - Mise en œuvre de l'association-type Administrer
Les ingénieurs maîtrisent donc des SGBD, ils sont affectés chez des clients qui utilisent ces SGBD.
Les contraintes d'inclusion (symbolisées par la lettre I cerclée de rouge) sont là pour signifier
qu'un ingénieur ne peut être administrateur d'un SGBD
qu'à la condition de maîtriser celui-ci, qu'il ne peut être administrateur chez un client qu'à la condition
d'y être affecté et qu'il ne peut être administrateur chez un client que de SGBD utilisés par celui-ci.
Le MLD (Modèle Logique des Données) dérivé est le suivant :
.png)
Figure 5.2 - MLD - Mise en œuvre de l'association-type Administrer
Un instantané :
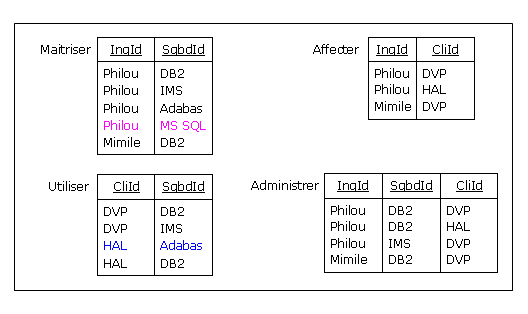
Figure 5.3 - Ingénieurs, SGBD, Clients : Administrer
On notera que le client HAL utilise Adabas, et qu'aucun ingénieur de la filiale de DVP
n'administre ce SGBD : chez LPABDD les commerciaux devront s'activer afin de combler cette lacune...
Considérons maintenant la double jointure naturelle (en Tutorial D) des relvars Maitriser, Utiliser et Affecter :
JOIN {Maitriser, Utiliser, Affecter} ;
Ou l'équivalent SQL :
SELECT x.IngId, y.SgbdId, z.CliId
FROM
Maitriser AS x
NATURAL JOIN Utiliser AS y
NATURAL JOIN Affecter AS z ;
Cette double jointure est cyclique (au sens de Codd) et produit la relation suivante, appelons-la MUA, dont Administrer
est ici un sous-ensemble strict (car le tuple <Philou, Adabas, HAL>
n'appartient pas à cette relation, nous y reviendrons) :
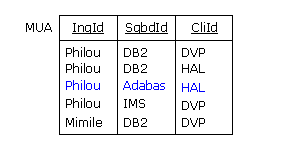
Figure 5.4 - Cycle entre Maitriser, Utiliser et Affecter
A cette relation (valeur) on ne peut pas associer de DMV non triviale. En effet :
|
La DMV {IngId} ➔➔ {SgbdId} | {CliId} n'est pas vérifiée pour MUA
puisqu'elle présuppose l'existence des tuples <Philou, IMS, HAL> et <Philou, Adabas, DVP>,
lesquels sont absents de MUA.
La DMV {SgbdId} ➔➔ {IngId} | {CliId} n'est pas non plus vérifiée
puisqu'elle présuppose l'existence du tuple <Mimile, DB2, HAL>, lequel est absent de MUA.
La DMV {CliId} ➔➔ {IngId} | {SgbdId} n'est pas non plus vérifiée
puisqu'elle présuppose l'existence du tuple <Mimile, IMS, DVP>, lequel est absent de MUA.
|
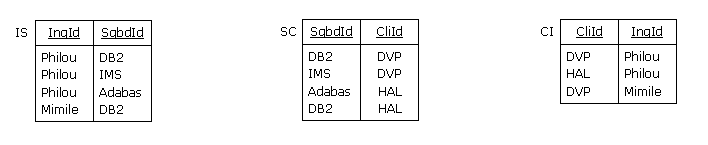
Mais si l'on projette MUA sur les paires IS {IngId, SgbdId}, SC {SgbdId, CliId} et
CI {CliId, IngId} :
Puis, si l'on effectue la jointure naturelle par exemple de IS et SC, on produit la relation ISC :
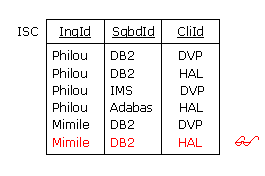
Du fait de la présence du tuple
<Mimile, DB2, HAL> dans ISC,
celle-ci est un surensemble strict de MUA, mais si l'on effectue la jointure naturelle de ISC et CI,
alors on évacue le tuple étranger et l'on retrouve la relation MUA (comme prévu par Codd en 1969) :
MUA =
JOIN {IS, SC, CI}.
Dans ces conditions, la relation MUA satisfait à la DJ suivante,
qui ne peut être ramenée à une
combinaison de DMV non triviales (on a montré que MUA en était dépourvue) :
★{{IngId, SgbdId}, {SgbdId, CliId}, {CliId, IngId}}
DJ qui exprime en fait la contrainte suivante :
Si <Philou, DB2>
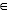
IS et <DB2, DVP>
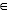
SC
et <DVP, Philou>
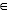
CI
alors <Philou, DB2, DVP>
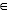
MUA
(A ce sujet, on pourra utilement se reporter à [Date 2004], paragraphe 13.3
« Join Dependencies and Fifth Normal Form » ou à [Date 2009], Appendice B
« Database Design Theory », paragraphe « More on 5NF »).
Supposons maintenant que les choses évoluent chez LPABDD et que la
maîtrise d'ouvrage décide de faire de cette contrainte une règle de gestion. Dans le dossier de
conception, on la réécrira sous une forme plus digeste pour l'utilisateur :
Si un ingénieur maîtrise un SGBD utilisé par un client chez qui il affecté,
alors cet ingénieur administre ce SGBD chez ce client.
Mais la relation Administrer de la figure 5.3 n'est alors plus valide. En effet Philou maîtrise Adabas
et il est affecté chez HAL qui utilise Adabas : il y manque le tuple
<Philou, Adabas, HAL>
et pour respecter la nouvelle règle de gestion on devra l'ajouter (pour retrouver ainsi MUA).
Suite à cet ajout, la relation Administrer ci-dessous est conforme à la nouvelle règle de gestion :
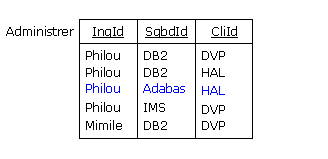
Figure 5.5 - Relation Administrer complétée
Mais désormais chaque valeur (relation) prise par la relvar Administrer fait double emploi avec la valeur
prise dans le même temps par la jointure naturelle MUA des relvars Maitriser, Utiliser et Affecter
(en notant qu'Administrer vérifie donc elle aussi la DJ
★{{IngId, SgbdId}, {IngId, CliId}, {SgbdId, CliId}}) :
il est inutile de matérialiser Administrer et au besoin on se contentera d'en faire
une
vue (pour ne pas avoir
à modifier les programmes qui manipulent la relvar, conformément à la 9e des
12 règles de Codd).
En tant que relvar de base, Administrer peut disparaître du MLD (et doit même disparaître, cf. paragraphe 5.4),
tandis qu'à son tour le diagramme conceptuel (Figure 5.1) devient le suivant :
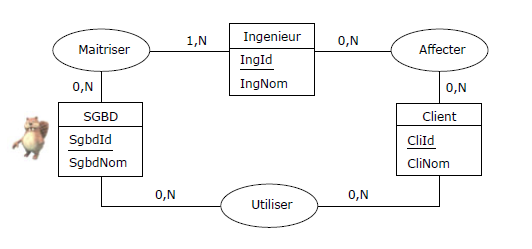
Figure 5.6 - Élimination de l'association-type Administrer
 |
A noter que, pour sa part, la relation IS {IngId, SgbdId} n'est pas égale à la relation Maitriser {IngId, SgbdId},
celle-ci comportant un tuple <Philou, MS SQL> n'appartenant pas à IS
qui n'est donc qu'un sous-ensemble, une restriction de Maitriser (conformément à la contrainte d'inclusion de la figure 5.1).
Par conséquent, qu'elle soit de base ou dérivée (vue), la relvar Administrer n'est pas décomposable en Maitriser,
Affecter, Utiliser, tandis qu'elle en est la jointure naturelle, mais ceci n'a aucune incidence sur les règles
de gestion précédemment énoncées.
|
Nota bene. Pour l'anecdote, en remplaçant le trio Ingenieur, SGBD, Client par le suivant : Fournisseur,
Produit, Projet, on retrouve l'exemple donné par Codd en 1969, dans lequel les fournisseurs pourvoient en
produits, lesquels sont utilisés pour des projets (voir aussi [Date 2004] au paragraphe 13.3
« Join Dependencies and Fifth Normal Form »).
On peut aussi considérer que ce trio correspond à celui de Nicolas ([Nicolas 1978]) et
repris par Fagin, les acteurs étant cette fois-ci des VRP multicartes proposant à la clientèle des produits fabriqués
par les entreprises qu'ils représentent.
A l'attention des merisiens : On peut encore considérer qu'il s'agit d'une autre transposition, celle de
l'exemple proposé dans [Tabourier 1986] : des personnes pénètrent dans des bâtiments,
conduisent des voitures, lesquelles sont garées dans les bâtiments. Yves Tabourier a réussi à
traiter des dépendances de jointure (et de la 5NF), sans en faire mention, tout comme pour
les dépendances multivaluées et la 4NF (cf. paragraphe 4.10). Well done! Mr. Tabourier...
5.4. Dépendance de jointure triviale
Soit X1, X2, ..., Xn des sous-ensembles d'attributs de l'en-tête H d'une relvar R vérifiant la DJ
★{X1, X2, ..., Xn}. Cette DJ est triviale si et seulement si
au moins un des sous-ensembles X1, X2, ..., Xn, a pour éléments l'ensemble des attributs de H.
Par exemple, comme on l'a vu, la relvar MUA (cf. Figure 5.4) vérifie la DJ :
★{{IngId, SgbdId}, {IngId, CliId}, {SgbdId, CliId}}
mais celle-ci n'est pas triviale
car ses éléments {IngId, SgbdId}, {IngId, CliId} et {SgbdId, CliId} sont tous des sous-ensembles
stricts de l'en-tête de MUA. Même chose pour la relvar Administrer « complétée » (cf. Figure 5.5).
 |
Le concept de dépendance de jointure triviale intervient dans la définition de la 5NF et dans
celle de la 6NF.
|
5.5. Définition de la 5NF (PJ/NF)
La définition donnée par Fagin :
N.B. R* représente l'en-tête de la relvar R. « Δ
 σ
σ » se lit ainsi :
Δ
implique logiquement σ, ou encore
σ est une conséquence logique de Δ.
Par ailleurs une dépendance de clé est une dépendance fonctionnelle K ➔ X vérifiée par R,
telle que X représente l'ensemble des attributs de R : K est donc une clé de R.
Pour en revenir à la relvar Administrer dans sa version « complétée » (cf. Figure 5.5) :
-
Elle fait l'objet de la DJ non triviale ★{{IngId, SgbdId}, {IngId, CliId}, {SgbdId, CliId}} ;
-
Elle a pour unique clé candidate K = {IngId, SgbdId, CliId}, car aucun des sous-ensembles stricts
{IngId, SgbdId}, {IngId, CliId} et {SgbdId, CliId} ne vérifie la propriété d'unicité des clés.
Comme aucun des sous-ensembles {IngId, SgbdId}, {IngId, CliId} et {SgbdId, CliId} de la DJ
ne contient K, la relvar ne respecte pas la 5NF.
Normaliser consiste alors à la remplacer par ses projections {IngId, SgbdId},
{IngId, CliId} et {SgbdId, CliId}. Comme on dispose déjà des relvars Maitriser, Affecter et Utiliser
qui en sont des sur-ensembles, on se contentera d'éliminer purement et simplement la relvar Administrer,
comme dans le cas de la Figure 5.6.
Si malgré tout on devait conserver cette relvar, toujours eu égard à la 9e des 12 règles de Codd,
ça devrait être seulement sous forme de vue. Par exemple, en Tutorial D :
VAR Administrer VIRTUAL
(JOIN {Maitriser, Utiliser, Affecter})
KEY {IngId, SgbdId, CliId)} ;
Si le chef n'aime pas les vues (ça arrive) et qu'il faille donc mettre en œuvre Administrer sous forme
d'une relvar de base, alors il deviendrait indispensable de mettre en œuvre
une contrainte pour s'assurer de la pérennité de la DJ non triviale :
★{{IngId, SgbdId}, {SgbdId, CliId}, {CliId, IngId}}
En Tutorial D :
CONSTRAINT Administrer_Contrainte_01
Administrer = JOIN {Maitriser, Utiliser, Affecter} ;
En SQL, il faudrait en passer par une assertion (ou des triggers si le SGBD ne connaît pas les assertions).
5.6. Exemples de relvars respectant ou non la 5NF
On vient de voir que la relvar Administrer « complétée » ne respecte pas la 5NF (alors qu'elle respecte la 4NF),
conséquence de la mise en application de la règle de gestion selon laquelle « Si un ingénieur
maîtrise un SGBD utilisé par un client chez qui il affecté, alors cet ingénieur administre ce SGBD chez ce client ».
En revanche, tant que cette règle n'existait pas (cf. Figure 5.1 et suivantes), la relvar Administrer respectait la 5NF.
En effet, la jointure de ses projections avait pour résultat une relation comportant un corps étranger
(cf. Figure 5.4), à savoir le tuple <Philou, Adabas, HAL> ne figurant pas
dans la relation Administrer de la Figure 5.3 :
la DJ ★{{IngId, SgbdId}, {SgbdId, CliId}, {CliId, IngId}} n'existait pas.
Pour leur part, les relvars Maitriser, Affecter et Utiliser dont on a des instantanés dans la Figure 5.3 respectent la 5NF.
Prenons le cas de la relvar Maitriser :
la seule DJ qu'elle comporte ★{{IngId, SgbdId}} est triviale
puisque l'en-tête de la relvar est la paire {IngId, SgbdId} (qui représente aussi la seule clé de la relvar).
Ce qui vaut pour Maitriser vaut aussi pour Affecter et Utiliser, mutatis mutandis.
Autre exemple : considérons la relvar FPV étudiée notamment aux paragraphes 3.2.2 et 3.3.3.
Elle satisfait à la DJ ★{FV, FPQ} puisqu'elle est égale à la jointure des relvars FV et FPQ
(cf. paragraphe 3.3.3). Elle a pour seule clé la paire {Four_No, Piece_No},
paire qui n'appartient pas à FV, en conséquence de quoi FPV ne respecte
pas la 5NF (on savait du reste qu'elle ne respecte même pas la 2NF, cf. paragraphe 3.4.2).
En revanche, la relvar FV {Four_No, Ville} ayant pour clé {Four_No} n'est pas décomposable sans perte, et a pour seule
DJ ★{{Four_No, Ville}}
laquelle est triviale (tout en notant que la clé {Four_No} est évidemment incluse dans {Four_No, Ville}).
La relvar FV respecte la 5NF.
De même (toujours au paragraphe 3.3.3), la relvar FPQ {Four_No, Piece_No, Quantite} ayant pour clé {Four_No, Piece_No}
n'est pas décomposable sans perte.
Elle a pour seule DJ ★{{Four_No, Piece_No, Quantite}} laquelle est triviale : la relvar respecte donc la 5NF.
Prenons un autre exemple, celui d'une relvar en 2NF mais pas en 3NF. Soit la relvar suivante :
Salarie {SalId, EntId, EntNom}
(clé soulignée)
L'attribut SalId représente l'identifiant (au sens Merise) d'un salarié, EntId représente l'identifiant
de l'entreprise de ce salarié et EntNom le nom de cette entreprise.
Les DF sont les suivantes :
DF1 {SalId} ➔ {EntId, EntNom}
DF2 {EntId} ➔ {EntNom}
Par application du théorème de Heath et de la règle de Rissanen de préservation des dépendances
(cf. paragraphe 3.3.2), la relvar Salarie peut être décomposée sans perte selon les projections :
{SalId, EntId}
(clé soulignée)
{EntId, EntNom}
(clé soulignée)
Étant décomposable sans perte, la relvar Salarie satisfait à la
DJ non triviale ★{{SalId, EntId}, {EntId, EntNom}}.
Elle a pour unique clé {SalId}, et comme le sous-ensemble {EntId, EntNom}
n'est pas clé de la relvar, celle-ci ne respecte pas la 5NF.
Encore un exemple, celui d'une relvar respectant la BCNF mais pas la 4NF. Soit la relvar
ISPV de la Figure 4.3 et décortiquée notamment dans les paragraphes 4.3 et 4.7 :
ISPV {IngId, SgbdId, ProjId, Annee}
ISPV a pour seule clé {IngId, SgbdId, ProjId, Annee}.
Elle comporte les DMV {IngId} ➔➔ {SgbdId}
et {IngId} ➔➔ {ProjId, Annee}.
ISPV satisfait donc à la DJ ★{{IngId, SgbdId}, {IngId, ProjId, Annee}},
Or, ni {IngId, SgbdId} ni {IngId, ProjId, Annee} ne sont clés de ISPV :
cette relvar ne respecte pas la 5NF (comme on l'a rappelé, elle ne respectait déjà pas la 4NF).
5.7. Parallèle entre la BCNF, la 4NF et la 5NF
Fagin fournit un parallèle très intéressant et élégant entre la BCNF, la 4NF et la 5NF.
Date l'a résumé ainsi ([Date 2004]) :
 Une relvar R est en BCNF si et seulement si chaque DF à laquelle elle satisfait est impliquée par les clés candidates de R.
Une relvar R est en BCNF si et seulement si chaque DF à laquelle elle satisfait est impliquée par les clés candidates de R.
 Une relvar R est en 4NF si et seulement si chaque DMV à laquelle elle satisfait est impliquée par les clés candidates de R.
Une relvar R est en 4NF si et seulement si chaque DMV à laquelle elle satisfait est impliquée par les clés candidates de R.
 Une relvar R est en 5NF si et seulement si chaque DJ à laquelle elle satisfait est impliquée par les clés candidates de R.
Une relvar R est en 5NF si et seulement si chaque DJ à laquelle elle satisfait est impliquée par les clés candidates de R.
|
5.8. Un autre théorème de Date et Fagin
Si une relvar est en 3NF et si chacune de ses clés candidates ne comporte qu'un seul attribut,
alors cette relvar est en 5NF.
|
Ce théorème de
Date et Fagin (théorème 4.1)
est utile, il permet en effet de restreindre la liste des relvars à vérifier, puisque celles dont les
clés sont seulement mono-attributs et qui sont en 3NF sont de facto en 5NF...
Encore un théorème en passant (cf. [Date 2009] page 296) :
Ce théorème est intéressant lui aussi, car il concerne des situations fréquemment rencontrées. Attention quand même
à ce qu'un attribut non-clé soit la conséquence d'une règle de gestion authentique. A défaut, si on
dotait par exemple la relvar Administrer d'un attribut technique (attribut d'audit, dans le genre de
la date d'insertion du tuple, etc.), une relation telle que celle de la Figure 5.5 ne serait plus décomposable.
Cette remarque rejoint celle qui figure en fin du paragraphe 4.8, concernant les clés primaires ne comportant
systématiquement qu'un seul attribut.
5.9. Pour conclure avec la normalisation en 5NF
Si l'on se plonge directement dans les écrits de Fagin, Ullman, Delobel, Maier, Zaniolo et autres chercheurs,
la normalisation apparaît comme un sujet très formalisé, mathématisé, faisant l'objet de nombreux théorèmes
pas toujours faciles à redémontrer, et l'on peut avoir tendance à se désintéresser du sujet. Heureusement, Chris Date
présente les choses de façon claire, didactique, précise et strictement conforme à la théorie fournie par ces
chercheurs (cf. [Date 2004]). En tout état de cause, nous disposons des outils permettant de contrôler
le respect de la 5NF. La méthode qui consiste à chercher les DF, DMV et DJ, ainsi que les clés, puisque celles-ci
doivent impliquer ces dépendances, peut être qualifiée d'ascendante, conduisant à décomposer par projection des relvars
non normalisées en relvars qui le deviennent. La démarche descendante, à laquelle tient tellement Yves Tabourier
(cf. paragraphe 4.13) est évidemment celle qu'il faut privilégier car elle permet d'évacuer à la pelle les
dépendances multivaluées et les dépendances de jointure, mais il n'empêche qu'il faut prouver que chaque relvar
de base (entité-type ou association-type en Merise) est normalisée, d'où une part de démarche ascendante inévitable.
Si celui qui a la compétence au niveau conceptuel mais ne l'a pas au niveau relationnel,
c'est-à-dire le concepteur au sens classique du terme, tient à ce que ses MCD et diagrammes de classes soient
irréprochables quant à la normalisation, le mieux — une fois son travail de modélisation
en bonne voie d'achèvement — est qu'il s'associe avec celui qui jongle avec les DF, DMV et DJ,
afin de procéder à une relecture à deux des règles de gestion des données, pour :
 Débusquer les anomalies potentielles restantes (redondances, anomalies en mise à jour),
Débusquer les anomalies potentielles restantes (redondances, anomalies en mise à jour),
 Améliorer encore les modèles conceptuels afin que ceux-ci puissent évoluer plus tard sans problème,
Améliorer encore les modèles conceptuels afin que ceux-ci puissent évoluer plus tard sans problème,
 Simplifier la mise en oeuvre des contraintes d'intégrité.
Simplifier la mise en oeuvre des contraintes d'intégrité.
|
Comme nous l'avons déjà fait observer, quelque part la normalisation a un côté yoyo...
Une fois le travail de normalisation achevé, on peut être amené à projeter une
relvar respectant la 5NF selon deux relvars ou plus (verticalement et/ou horizontalement), mais on entre
là dans des considérations relevant pour l'essentiel :
non_indente.jpg) |
De la gestion de données intervallaires, disons temporelles et qui intéressent la 6NF (cf. paragraphe 6) ;
|
non_indente.jpg) |
De l'optimisation (cf. paragraphe 1.7) : par exemple, certains
attributs de cette relvar sont seulement consultés par une population X d'utilisateurs, tandis que d'autres attributs
sont mis à jour par une population différente Y d'utilisateurs, et les contentions qui en résultent sont pénalisantes
pour les premiers, ce qui amène en l'occurrence à encore décomposer des structures qui sont déjà en 5NF
(dans le sens de la 6NF soit dit en passant).
|
La normalisation des relvars n'est évidemment pas la panacée et peut être source de dilemmes, quand elle
peut faire perdre des règles de gestion, comme on l'a vu avec la BCNF (cf. paragraphe 3.7),
ou avec la 4NF (cf. paragraphe 4.9). Heureusement, ce genre de situation est rare et — d'expérience —
provoque en général une remise en cause des règles de gestion impliquées.
Bref, normalisons, normalisons, normalisons et les applications s'appuieront sur des bases de données saines.
Et attention à ce que l'on peut glaner sur la Toile ou dans des ouvrages écrits par des « experts »
(sic), gens peut-être convaincus et pleins de bonne volonté, mais ayant une connaissance insuffisante
du sujet, n'ayant pas étudié les bons auteurs et n'ayant manifestement pas véritablement transpiré sur des projets
d'une certaine importance, nécessitant une revue rigoureuse et pertinente. Voir ci-dessous les considérations
de l'« expert » de service déjà épinglé (cf. paragraphe 2.8)...
5.10. Un petit exercice
A titre d'exercice, je vous invite à recenser et commenter les erreurs contenues dans le texte suivant,
ayant pour titre :
|
« Les Quatrième et Cinquième Formes Normales ne sont pas incluses dans la Troisième Forme Normale »
« Tous les auteurs affirment que ces deux dernières Formes Normales sont incluses dans la Troisième,
prolongeant de façon mécanique la série d'inclusion entre les Troisième, Deuxième et Première Formes Normales.
Nous allons montrer que cette affirmation est fausse, car elle gêne énormément la compréhension des Quatrième
et Cinquième Formes Normales.
S'il est exact que la Troisième Forme Normale est incluse dans la Deuxième et elle-même dans la Première,
le simple bon sens permet de voir que la Quatrième n'est pas incluse dans la Troisième.
En effet, les trois premières Formes Normales sont fondées sur les Dépendances Fonctionnelles alors que la
Quatrième (comme la Cinquième) s'appuie sur les Dépendances Multivaluées. Or, la Dépendance Fonctionnelle
est un cas particulier de la Dépendances Multivaluée. On peut donc considérer qu'elle est incluse dans
dans cette dernière, mais en aucun cas l'inverse. Donc la Quatrième Forme Normale ne peut être incluse dans
la Troisième ; tout au plus pourrait-on admettre l'inverse : que la Troisième soit incluse dans la Quatrième. »
... (Au passage une critique à l'endroit des chercheurs (cf. paragraphe 2.8), puis reprise des explications.)
« En fait un Tableau en Quatrième Forme Normale n'est pas en Troisième Forme Normale, ni même en Deuxième,
tout simplement parce qu'il n'est pas en Première Forme Normale. En effet, la condition essentielle pour
qu'un Tableau soit en Première Forme Normale est l'existence d'une Clef.
Une Clef est une Colonne ou un groupe de Colonnes identifiant toutes les autres de façon unique, c'est-à-dire
qu'elle est à l'origine des Dépendances Fonctionnelles. Or, dans un tableau en Quatrième Forme Normale,
il n'existe aucune Dépendance Fonctionnelle, seulement une Dépendance Multivaluée.
Il n'y a pas de Clef dans un Tableau en Quatrième Forme Normale, et celui-ci n'est donc pas en Première Forme Normale.
Le processus de Normalisation que nous venons de détailler a donc pour but de se prémunir contre la redondance
d'informations et contre les difficultés de mise à jour. Lorsqu'il est conduit à son terme, ne subsistent
que deux types de Tableaux :
— Des Tableaux en Forme Normale de Boyce-Codd, c'est-à-dire en Troisième Forme Normale avec, éventuellement,
Normalisation de Boyce-Codd ;
— Des Tableaux Binaires exprimant chacun une Dépendance Multivaluée Elémentaire. »
|
Fermez le ban.
Vous pouvez aussi relever le peu qui soit pertinent, mais si vous avez échoué dans le démontage de cet énorme sophisme,
prenez la peine de repasser par la case Départ.
N.B. Il est fait mention de la dépendance multivaluée élémentaire : pour l'auteur
« la Dépendance Multivaluée est Elémentaire seulement si l'Identifiant est constitué
d'une seule Colonne ». Quant à l'Identifiant, il précise qu'il s'agit d'une colonne
(ou d'un ensemble de colonnes), dont une autre colonne est dépendante : il s'agit donc du déterminant
d'une dépendance multivaluée (ou fonctionnelle), rien à voir l'identifiant au sens Merise du terme.
Bonne chasse.


Copyright © 2008 - François de Sainte Marie.
Aucune reproduction, même partielle, ne peut être faite
de ce site ni de l'ensemble de son contenu : textes, documents, images, etc.
sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à
trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.


.png)
.png)



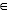 IS et <DB2, DVP>
IS et <DB2, DVP> 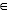 SC
et <DVP, Philou>
SC
et <DVP, Philou> 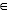 CI
alors <Philou, DB2, DVP>
CI
alors <Philou, DB2, DVP> 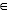 MUA
MUA





.png)
 σ » se lit ainsi :
Δ implique logiquement σ, ou encore σ est une conséquence logique de Δ.
Par ailleurs une dépendance de clé est une dépendance fonctionnelle K ➔ X vérifiée par R,
telle que X représente l'ensemble des attributs de R : K est donc une clé de R.
σ » se lit ainsi :
Δ implique logiquement σ, ou encore σ est une conséquence logique de Δ.
Par ailleurs une dépendance de clé est une dépendance fonctionnelle K ➔ X vérifiée par R,
telle que X représente l'ensemble des attributs de R : K est donc une clé de R.
 Une relvar R est en BCNF si et seulement si chaque DF à laquelle elle satisfait est impliquée par les clés candidates de R.
Une relvar R est en BCNF si et seulement si chaque DF à laquelle elle satisfait est impliquée par les clés candidates de R.
 Une relvar R est en 4NF si et seulement si chaque DMV à laquelle elle satisfait est impliquée par les clés candidates de R.
Une relvar R est en 4NF si et seulement si chaque DMV à laquelle elle satisfait est impliquée par les clés candidates de R.
 Une relvar R est en 5NF si et seulement si chaque DJ à laquelle elle satisfait est impliquée par les clés candidates de R.
Une relvar R est en 5NF si et seulement si chaque DJ à laquelle elle satisfait est impliquée par les clés candidates de R.

 Débusquer les anomalies potentielles restantes (redondances, anomalies en mise à jour),
Débusquer les anomalies potentielles restantes (redondances, anomalies en mise à jour),
 Améliorer encore les modèles conceptuels afin que ceux-ci puissent évoluer plus tard sans problème,
Améliorer encore les modèles conceptuels afin que ceux-ci puissent évoluer plus tard sans problème,
 Simplifier la mise en oeuvre des contraintes d'intégrité.
Simplifier la mise en oeuvre des contraintes d'intégrité.
non_indente.jpg)
non_indente.jpg)