Bases de données relationnelles et normalisation :
de la première à la sixième forme normale
Date de publication : 07/09/2008. Date de mise à jour : 14/07/2012.
1. De la normalisation
1.1. Contexte
1.2. Retour aux sources
1.3. Rappel de quelques définitions
1.4. Objet de la normalisation
1.5. Étapes de la normalisation
1.6. Normaliser, une obligation ?
1.7. Dénormalisation vs amélioration (optimisation)
1. De la normalisation
1.1. Contexte
Quand on parle de bases de données relationnelles, on évoque immanquablement les trois piliers
qui constituent les fondements de la théorie relationnelle et ayant pour objet :
-
La structure des données, c'est-à-dire, si l'on se situe au niveau SQL, les règles de définition
des tables en termes de lignes et de colonnes ;
-
La manipulation des données : comment exploiter ces tables, à l'aide par exemple — toujours
dans le contexte SQL — de l'incontournable triplet SELECT, FROM, WHERE et des opérateurs INSERT, etc. ;
-
L'intégrité des données, c'est-à-dire les moyens mis à notre disposition par le SGBD,
concourant à la validité de ces données, tels que les clés primaires, clés étrangères, et contraintes diverses
(assertions et triggers si SQL...)
Il existe par ailleurs un volet extrêmement important concernant les bases de données relationnelles,
celui de la normalisation, dont l'objet est double :
-
A l'intersection d'une ligne et d'une colonne, certes on trouve des données de type très simple,
telles que les habituels
nombres et chaînes de caractères, mais peut-on aussi légalement trouver des données de types plus complexes,
telles que des listes, des tableaux, des tables, etc. ? La normalisation a pour objet de confirmer les règles
du jeu à ce sujet, en relation avec les effets que cela peut avoir sur chacun des trois piliers précédents.
Cela concerne au premier chef ce qu'il est convenu d'appeler la Première Forme Normale (1NF) et sera développé
dans le paragraphe 2 « Première forme normale ».
-
La normalisation a aussi pour objet de fournir les outils et les techniques nous permettant de débusquer,
d'éliminer les redondances qui non seulement rendent les tables obèses, mais par ailleurs nous compliquent
la vie lors des opérations qui les mettent à jour (mises à jour nécessairement redondantes elles aussi)
finissant par rendre
faux le contenu de la base de données, sans parler de l'effet néfaste sur les performances. Par voie de conséquence,
en normalisant, tout en éliminant ce genre d'impedimenta, on améliore l'architecture de la base de données,
ce qui n'est pas un mince avantage, ne serait-ce que si l'on a un jour à faire évoluer celle-ci.
Cela concerne les formes normales suivantes (2NF à 5NF) et sera développé dans les paragraphes 3 et suivants.
Vu sa spécificité (garde-fou dans la manipulation des données intervallaires), la 6NF sera traitée
dans le contexte de la modélisation des données temporelles.
L'objet de la normalisation est repris dans le paragraphe 1.4.
1.2. Retour aux sources
Tout d'abord, il sera régulièrement fait ici référence à Ted Codd (1923-2003), le génial inventeur du
Modèle Relationnel de Données, qui a tout de suite traité de la normalisation, de manière très rigoureuse.
Ensuite, bien que Ted Codd ne traite que des relations, suivant le contexte, on utilisera aussi
par la suite les termes « table » et « relvar » (voir ci-dessous :
« Relvar, relation et table »).
En attendant, commençons par rappeler ce qu'est une relation dans le cadre de la théorie relationnelle.
Alors que SQL n'était pas encore né, et pour cause — et a fortiori le concept SQL de table —
voici la définition donnée par Ted Codd de la relation dans son article fondateur (cf. [Codd 1970], paragraphe 1.3) :
|
« Le terme relation est utilisé ici dans son acception mathématique.
Étant donnés les ensembles S1, S2, ..., Sn (non nécessairement distincts),
R est une relation sur ces n ensembles si c'est un ensemble de n-uplets,
le 1er élément de chacun d'eux tirant sa valeur de S1, le 2e de S2, et ainsi de suite
(de manière plus concise, R est un sous-ensemble du produit cartésien S1 X S2 X ... X Sn).
On fera référence à Sj comme étant le jième domaine de R. Suite à ce qui vient d'être énoncé, on dit que
R est de degré n. Les relations de degré 1 sont souvent dites unaires, celles de degré 2 binaires, de degré 3 ternaires,
et celles de degré n n-aires. »
|
Une représentation imagée d'un n-uplet d'une relation R de degré n,
construit sur les domaines S1, S2, ..., Sn :

Figure 1.1 - Un n-uplet, comme des perles qu'on enfile
Codd poursuit :
|
« Pour simplifier l'exposé, on utilisera souvent une représentation des relations sous forme de tableaux ...
Un tableau représentant une relation a les propriétés suivantes :
.jpg) (1) Chaque ligne représente un n-uplet de R,
(1) Chaque ligne représente un n-uplet de R,
.jpg) (2) L'ordre des lignes n'a aucune importance,
(2) L'ordre des lignes n'a aucune importance,
.jpg) (3) Toutes les lignes sont distinctes,
(3) Toutes les lignes sont distinctes,
.jpg) (4) L'ordre des colonnes est significatif —
il correspond à l'ordre S1, S2, ..., Sn des domaines sur lesquels sont définis les domaines de R.
(4) L'ordre des colonnes est significatif —
il correspond à l'ordre S1, S2, ..., Sn des domaines sur lesquels sont définis les domaines de R.
.jpg) (5) La signification de chaque colonne
est en partie rendue en l'affectant du nom du domaine correspondant. »
(5) La signification de chaque colonne
est en partie rendue en l'affectant du nom du domaine correspondant. »
|
Représentation d'une relation R de degré n, sous forme imagée, rectangulaire, plate et traditionnelle :

Figure 1.2 - Une relation sous forme de tableau
 |
Mais attention, l'image n'est pas la chose !
|
Dans ce qu'a écrit Codd, un point important peut paraître aujourd'hui choquant : il est en effet précisé que
l'ordre des colonnes est significatif (point 4).
Cela vient du fait que, dans ce tout premier jus du Modèle Relationnel, une colonne n'a pas de nom en propre,
elle hérite implicitement de celui de son domaine de référence : contexte mathématique oblige.
Ce n'est qu'en 1971 (cf. [Codd 1971], page 31)
qu'apparaît le concept d'attribut, débarrassant le Modèle Relationnel de cette fâcheuse contrainte.
Je cite (en rappelant que l'avatar SQL de la relation est la table et que le
degré d'une relation correspond au nombre de colonnes d'une table) :
|
« Les n domaines ne sont pas nécessairement distincts. Plutôt qu'utiliser un ordre pour déterminer chaque domaine
référencé (comme cela se fait en mathématiques), on utilisera un nom distinct pour chaque
référence faite et nous l'appellerons nom de l'attribut... En conséquence, chaque
référence faite à un domaine lors de la définition de R est appelée attribut de R.
Par exemple, une relation de degré 3 pourrait avoir pour attributs (A1, A2, A3) tandis que les domaines
correspondants pourraient être les domaines (D5, D7, D5). Les noms d'attributs sont un moyen d'éviter d'imposer aux utilisateurs
la connaissance de la position des domaines. »
|
1.3. Rappel de quelques définitions
Les définitions qui suivent reprennent celles de Chris Date (cf. le paragraphe A en annexe).
non_indente.jpg) |
Un domaine tel que Sj est un ensemble de valeurs, par exemple celui des entiers, celui des chaînes de caractères,
ceux des dates, des points, des lignes, des ellipses, polygones, des numéros de Siret, des codes postaux,
des ISBN, des EAN13, etc.
A noter qu'aujourd'hui on utilise le terme type plutôt que le terme domaine.
|
non_indente.jpg) |
Un n-uplet (ou tuple) est une valeur. C'est un ensemble de triplets de la forme <Ai, Di, vi>
où Ai désigne un nom d'attribut, Di désigne un nom de domaine et vi une valeur appartenant au domaine Di.
Le couple <Ai, Di> est un attribut du n-uplet ; vi est la valeur d'attribut de l'attribut Ai ;
le domaine Di en est le domaine d'attribut correspondant (type d'attribut).
Exemple graphique, plat : un n-uplet composé des triplets <Attr1, D1, a11>, <Attr2, D2, a21>, ...,
<Attrn, Dn, an1>
|

Figure_1.3a - Un n-uplet au format tabulaire
|
Autre exemple plus parlant de n-uplet : un certain membre chez Developppez.com
|
.png)
Figure 1.3b - Autre exemple de n-uplet au format tabulaire
non_indente.jpg) |
Une relation est une valeur. Plus précisément, c'est une valeur constituée d'un en-tête
(ou schéma ou intension, notez l'orthographe) et d'un corps (extension).
L'en-tête est composé d'un ensemble d'attributs. Le corps est l'ensemble
des n-uplets composant la relation.
|
Exemple de représentation sous forme tabulaire d'une relation n-dimensionnelle (tout en rappelant que l'image
d'une chose n'est pas la chose) :

Figure 1.4 - Composants d'une relation
Dans un contexte informel, il est courant de ne pas faire figurer le nom des domaines
dans [l'image de] l'en-tête :
Figure 1.5 - Représentation informelle d'une relation
Relvar, relation et table
Au vu de ces représentations, on pourrait penser qu'une table SQL est une relation
(en remplaçant les termes « attribut » et « n-uplet » respectivement
par « colonne » et « ligne »).
Ça n'est pas exactement le cas, car (outre bon nombre de propriétés non nécessairement partagées) une
table peut changer de valeur, tandis qu'une relation est une valeur, donc par définition
invariable, tout comme les entiers 1 ou 2. L'aspect variable des choses concerne la
variable relationnelle (en abrégé relvar), type de variable affectée successivement
de valeurs qui sont des relations : une relation y remplace une autre lors d'une opération de
mise à jour. Notons que Codd n'utilisait pas le terme relvar, mais l'expression « time-varying relation »,
qui n'est plus jugée pertinente aujourd'hui, du fait du caractère justement invariable des relations.
Et n'oublions pas qu'une table SQL peut n'être qu'un sac (bag), dans la mesure où la présence d'une clé
(disons primaire) n'est pas exigée, ce qui autorise l'existence de lignes en double
(or un sac n'est pas un ensemble).
1.4. Objet de la normalisation
a) A propos de la première forme normale (dont l'étude est développée dans le paragraphe 2).
Les relations sont des êtres mathématiques. Elles sont soumises à certaines contraintes structurelles
et leur finalité est d'être manipulées, combinées, à l'aide de l'
algèbre relationnelle ou
du
calcul relationnel (qui est une application
du calcul des prédicats). Ayant une préférence pour le calcul des prédicats, Ted Codd a raisonné en logicien.
Nous verrons à l'occasion de l'étude de la première forme normale, qu'en 1969, il se plaça d'entrée dans le cadre de la
logique du deuxième ordre, jugeant l'année suivante que la logique du premier ordre
suffisait pour manipuler les relations.
(1)
L'adéquation du calcul relationnel (et par contrecoup de l'algèbre relationnelle) à la logique du premier ordre eut
pour conséquence une contrainte forte, conduisant à normaliser les relations en ce qu'il est convenu d'appeler
la première forme normale (1NF), selon laquelle une relation ne peut pas être une valeur pour un attribut d'une
autre relation :
par exemple, les lignes de factures d'une facture ne peuvent pas être des valeurs d'un attribut LigneDeFacture d'une
relation Facture (voir toutefois le cas des RVA, au paragraphe 2.6).
Certes, avec des systèmes comme IMS/DL1, par construction (modèle hiérarchique oblige), les lignes de facture
sont nichées dans les factures, les engagements sur lignes de facture sont nichés dans les lignes de facture, etc.
Mais IMS/DL1 ne permet pas de manipuler des
ensembles à l'aide d'une algèbre ou d'un calcul,
on est à un niveau inférieur où l'on ne traite qu'
un enregistrement à la fois et, dans ces conditions,
il n'y a évidemment aucune contrainte quant à la façon de structurer les données.
b) A propos des autres formes normales (dont l'étude est développée dans les paragraphes 3 et suivants).
Ce que l'on appelle deuxième forme normale, troisième forme normale et forme normale de Boyce-Codd sont les
éléments d'une théorie, d'abord développée par Codd dès 1970, puis complétée par Raymond Boyce (trop tôt
disparu en 1974).
Sept ou huit ans après que Codd l'eut entamée, des mathématiciens comme Jorma Rissanen et Ronald Fagin prirent
le relais pour compléter la théorie de la normalisation, ce qui fut fait en 1979 avec la mise à notre
disposition des quatrième et cinquième formes normales (et de la sixième, vingt ans plus tard).
Pour reprendre ce qui a été évoqué au paragraphe 1.1,
respecter ces formes normales a pour effet (entre autres choses) de débarrasser les relations
de
redondances non seulement inutiles et causes d'obésité, mais surtout génératrices d'erreurs eu égard aux
règles de gestion des données de l'entreprise, lors des opérations de
mise à jour (disons INSERT, UPDATE, DELETE).
Ces redondances sont le plus souvent la conséquence d'une modélisation conceptuelle en amont maladroite,
voire inexistante, ou encore le mauvais fruit d'une « dénormalisation » inopportune (
horresco referens...)
c) Observations concernant la modélisation conceptuelle.
Lorsqu'on représente les données sous forme graphique : modèles conceptuels de données (MCD) de la méthode Merise,
et plus généralement diagrammes entités/relations (voire diagrammes de classes), il y a tout un travail de vérification
concernant chaque type d'association (ce qu'on désigne encore par association-type ou relation-type)
entre types d'entités, consistant à « s'assurer que chacune des propriétés ne peut être vérifiée sur un sous-ensemble
de la collection de la relation-type » [TRC 1989]. Attention, dans cette citation, la relation-type
en question n'a rien à voir
avec la relation du Modèle Relationnel, il s'agit de l'association (relationship) existant entre entités-types.
Ce travail de vérification — portant lui aussi le nom de normalisation — conduit à expulser au besoin
une propriété d'une association-type vers une entité-type (ou inversement). Ceci a à voir avec ce que
Codd appelle la normalisation en deuxième forme normale (2NF), laquelle a en vérité une portée bien plus étendue,
car elle concerne l'ensemble des relvars composant une base de données relationnelle. La 2NF est aussi
beaucoup plus formelle quant à son énoncé.
La normalisation joue un rôle crucial quant à la qualité de l'architecture de la base de données,
laquelle doit être structurellement valide et apte à évoluer, premièrement par le recours à une
démarche au niveau conceptuel synthétique, descendante (donc en amont), à l'aide
par exemple de la méthode Merise (démarche valant également pour les diagrammes de classes),
deuxièmement par une vérification rigoureuse, mettant en jeu une démarche analytique,
ascendante, pour laquelle on s'appuie justement sur la théorie de la normalisation :
l'architecture de la base de données relève ainsi d'une approche mixte où l'on pratique l'art du yoyo,
en alternant intelligemment les deux démarches.
d) Prise en compte des données temporelles (voir au paragraphe 6).
Ensemble, Hugh Darwen, Nikos Lorentzos et Chris Date, compagnon de route, fils spirituel
(et parfois rebelle) de Ted Codd, ont enrichi la théorie relationnelle, en approfondissant avec
une extrême rigueur le domaine des bases de données temporelles, et en nous fournissant les
techniques pour nous y lancer à notre tour, autrement qu'à l'instinct, comme c'est hélas trop
souvent le cas, ou sur la base de travaux théoriques jugés défectueux (cas de TSQL2 qui
fut en son temps proposé pour être intégré à la norme SQL/2).
C'est un sujet d'étude essentiel, que tous les concepteurs devraient approfondir,
car depuis toujours, la prise en compte du temps dans les bases de données a été, et reste quelque chose
de compliqué et d'omniprésent, au moins dans le monde mouvant et agité de l'assurance, de la banque,
de la grande distribution, de la retraite, et j'en passe.
 |
Maintenant, comme dit Chris Date :
« Normalization is no panacea but it's a lot better than the alternative! »
|
1.5. Étapes de la normalisation
L'usage veut que l'on normalise en procédant par étapes : dans un premier temps, on s'assure que l'on respecte
ce que l'on appelle la première forme normale (1FN ou 1NF) déjà évoquée (ceci concerne les tables SQL et
apparentées, car pour leur part les relvars sont de facto en 1NF).
Ensuite, on s'assure que chaque relvar (ou table SQL), respecte ce que l'on appelle la 2e forme normale
(2FN ou 2NF), puis la 3e forme normale (3FN ou 3NF), la forme normale de Boyce/Codd (FNBC ou BCNF),
la 4e forme normale (4FN ou 4NF), la 5e forme normale (5FN ou 5NF) encore appelée PJ/NF (Project/Join Normal Form,
forme normale par projection/jointure).
La projection et la jointure naturelle
(cf. le paragraphe B en annexe) sont les deux opérations utilisées
tout au long du processus (d'où l'expression « normalisation par projection/jointure »).
La projection est utilisée
pour remplacer une relvar R qui ne respecte pas la xNF par deux relvars (ou plus dans le cas de la 5NF)
R1 et R2 qui la respectent,
et la jointure naturelle est utilisée pour retrouver très exactement R à partir de R1 et R2 au cas où le besoin
s'en ferait sentir (par exemple au moyen d'une vue, ce qui permet de respecter le principe de
l'indépendance logique des données, en garantissant la simplification de la manipulation
des données par l'utilisateur, une stabilité de la représentation de celles-ci, tout à fait profitable
pour les applications, etc.)
Pour les données temporelles (plus généralement intervallaires), il est très vivement recommandé de pousser jusqu'à la
6e forme normale (6FN ou 6NF), qui marque la fin du processus de normalisation.
On notera qu'une relvar en 2NF est nécessairement en 1NF, qu'une relvar en 3NF est nécessairement en 2NF, etc.,
d'où la traditionnelle représentation graphique (enrichie de la 6NF) :
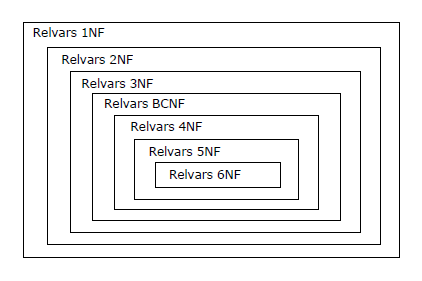
Figure 1.6 - Les relvars à la manière des matriochkas
Quand on a acquis un certain entraînement, on peut s'intéresser directement à la BCNF et se dispenser des étapes
consistant à s'assurer que l'on est en 2NF et 3NF. Quant à la 4NF et à la 5NF, la partie est réputée assez difficile
et l'on fait souvent l'impasse, en espérant que le MCD (modèle conceptuel de données) ou le diagramme de classes
que l'on a réalisés soient normalisés, ce qui est en principe le cas avec des concepteurs expérimentés, mais
gare quand même aux surprises (cf. paragraphe 4.11). Quant aux Sotomayor de la normalisation, ils placent la barre
à la hauteur de la BCNF histoire de d'échauffer, puis attaquent directement la barre de la 5NF.
Les barres intermédiaires ne les intéressent pas.
1.6. Normaliser, une obligation ?
Par construction chaque relvar d'une base de données respecte la 1NF, et chaque table SQL doit évidemment
en faire autant. Normaliser en 2NF et au-delà, est très vivement
recommandé, même si d'un point de vue théorique ça n'est pas une obligation stricte, dans la mesure
où l'algèbre relationnelle n'en subit pas les effets.
Mais nombreux sont ceux qui, sous l'emprise de l'émotion ou par crédulité (lecture de la presse du coeur informatique,
ragots de cafétéria, influence des légendes en tous genres colportées depuis l'arrivée des premiers SGBDR ...),
préconisent une
non-normalisation a priori et se limitent au respect de la 1NF.
En effet, la normalisation conduit à casser une relvar en deux ou plusieurs relvars,
en conséquence de quoi, « dénormaliser » (réassembler les morceaux) serait synonyme d'
optimiser.
Ceux-là devraient avoir à l'esprit cette réflexion de
Donald Knuth
(qui l'a peut-être empruntée à Tony Hoare) :
« Premature optimization is the root of all evil. »
Quelques variantes des arguments avancés par les ignorants :
non_indente.jpg) |
A cause de la jointure, les requêtes deviendraient compliquées. Developpez.com abonde en commentaires
du genre : « D'accord, je vais faire comme vous dites, mais ça complique
les requêtes ». Pour sa part, le DBA se fera un plaisir d'encapsuler ces requêtes dans des vues,
lesquelles seront pour l'utilisateur des relvars comme les autres
(respect du principe de l'indépendance logique).
|
non_indente.jpg) |
Recomposer une relvar à partir des « morceaux » fait une fois de plus intervenir l'opération de
jointure, que l'on qualifie hâtivement de non performante, en toute méconnaissance
de cause, c'est-à-dire en confondant allègrement le niveau logique et le niveau physique.
Certes, selon un raisonnement simpliste et en se plaçant au niveau physique,
si les enregistrements impliqués ne sont pas dans la même page (bloc physique) sur le disque,
la jointure serait source d'accès au disque (ou au cache) supplémentaires, mais son statut
d'opération relationnelle par excellence fait qu'elle est l'objet de tous les soins de
l'optimiseur des SGBD relationnels dignes de ce nom et qu'il n'y a pas lieu de s'affoler.
Se reporter à ce sujet au paragraphe 3.8.
La jointure a bon dos, les problèmes de performance sont ailleurs.
|
Dénormaliser n'est pas interdit, mais on en connaît aussi les inconvénients, par exemple :
non_indente.jpg) |
Dégradation de la qualité de la modélisation que l'on finit par ne plus maîtriser et faire évoluer proprement.
|
non_indente.jpg) |
Nécessité de mettre en œuvre des contraintes (assertions ou triggers en SQL) garantissant sous le capot
le respect de certaines dépendances fonctionnelles, multivaluées, etc., qui sont les conséquences
du non respect de la normalisation.
|
non_indente.jpg) |
Anomalies potentielles de mise à jour, obésité des tables SQL due à l'inflation des redondances,
à leur enneigement (données utiles clairsemées, noyées au milieu de tombereaux de nulls — lesquels
ne facilitent pas la tâche des optimiseurs —, et de valeurs par défaut plus ou moins pertinentes).
|
non_indente.jpg) |
Parce qu'un SGBD comme DB2 ne respecte qu'en partie le principe de l'indépendance physique
(à chacun de voir ce qu'il en est quant à son SGBD favori), un tuple d'une relation (ligne d'une table)
est (physiquement) logé en totalité au sein d'un enregistrement sur le disque, c'est sommaire, mais c'est ainsi.
En conséquence, l'accès à une valeur d'attribut d'un tuple provoque l'accès à l'ensemble des valeurs
d'attributs de ce tuple. Suite à dénormalisation, la taille d'un enregistrement physique est supérieure
à celle des enregistrements « normalisés », ce qui fait qu'il y aura moins d'enregistrements
par page (bloc physique sur le disque). Ainsi, pour un traitement séquentiel par lots (batch)
ou pour des transactions lourdes, le nombre de lectures/écritures sera accru et la durée
du traitement en pâtira d'autant.
|
non_indente.jpg) |
Les opérations de mise à jour ne sont pas à l'abri : là encore, du fait du non respect de
l'indépendance physique, la mémoire sera inutilement encombrée et les temps de traitement pénalisés,
car le SGBD manipulera des enregistrements pondéralement surchargés.
|
Il faut descendre dans la soute et prouver le bien-fondé de cette dénormalisation,
résultats de mesures sérieuses en main, suite à des séances de prototypage de performance poussées.
Un exemple simple, celui qui est considéré au paragraphe 3.8 est caractéristique de
situations où l'on se trompe de cible, et dans lesquelles dénormaliser revient à appliquer
un cautère sur une jambe de bois sans améliorer la performance. Dénormaliser devient dangereux
(anomalies potentielles de mise à jour, coût du stockage), comme par exemple dans le cas de
l'hypothétique table des membres de DVP (cf. paragraphes 3.1.2 et 3.1.3). Une réflexion attentive
portant sur cette table (cf. Figure 3.2) incite à penser que c'est bien plus la dénormalisation
que la normalisation qui peut être source d'une inflation de lectures/écritures physiques sur disque
et d'encombrement des caches.
En passant : existe-t-il des règles logiques nous permettant de dénormaliser de façon rationnelle ?
En ce sens, je traduis Chris Date ([Date 2007b], chapitre 9, « Denormalization Considered Harmful » :
 |
« Je voudrais mettre l'accent sur un point : une fois que l'on a décidé de dénormaliser, on s'est engagé
sur une pente fort glissante. Question : Quand s'arrêter ? Avec la normalisation, la situation est
différente car on a des raisons logiques et claires de poursuivre le processus jusqu'à ce qu'on ait
atteint la forme normale la plus élevée possible. Doit-on en conclure qu'avec la dénormalisation on ait
à procéder jusqu'à atteindre la forme normale la moins élevée qui soit ? Bien sûr que non, à ce jour
nous ne disposons pas de critères logiques permettant de décider quand arrêter le processus.
En d'autres termes, en choisissant de dénormaliser, on a décidé d'abandonner une position qui offre une base
scientifique et une théorie logique solides, pour la remplacer par quelque chose de purement pragmatique
et nécessairement subjectif. »
|
Au fond, la dénormalisation est un bel exemple d'ignoratio elenchi.
Et comme le fait observer Frédéric Brouard (SQLpro) :
 |
« On peut aussi pousser le bouchon à l'extrême : pourquoi pas une seule table contenant tout dans la base ?
Vous commencez donc à douter de l'efficacité du tout au même endroit... Mais où il faut-il s'arrêter ?
Ou placer le curseur ? C'est justement l'art du respect des formes normales qui nous en donne la clef ! »
|
Signalons quand même une situation dans laquelle on peut cette fois-ci se poser légitimement la question de la
dénormalisation d'une relvar : il s'agit de la situation dans laquelle la BCNF ou la 4NF seraient violées,
alors que la normalisation à tout prix n'arrangerait pas forcément les choses (cf. paragraphes 3.7 et 4.9).
Mais il faut reconnaître que cette situation ne se présente
fort heureusement pas souvent. Sinon, si la modélisation conceptuelle des données est réalisée selon les
règles de l'art, on n'a guère de raison objective de ne pas normaliser :
 |
La dénormalisation est en général la conséquence d'une modélisation conceptuelle des données absente ou non maîtrisée.
|
Un dernier point. Si d'aucuns admettent que les bases de données utilisées dans un contexte transactionnel
doivent être normalisées, ils n'ont aucun état d'âme à dénormaliser à tout va les tables de
dimension dans le contexte des bases de données décisionnelles
(
Dimensional Modeling).
Si ces tables sont uniquement reconstruites (par exemple chaque nuit)
et ne font l'objet d'aucune mise à jour de type INSERT, UPDATE, DELETE entre deux
chargements, pourquoi pas... En tout cas, il y aura du
null, de la neige, de la redondance
difficilement contrôlable
malgré le soin extrême que l'on apportera aux opérations (
errare humanum est...)
Quoi qu'il en soit, les bases de données décisionnelles ne sont pas l'objet de cet article.
1.7. Dénormalisation vs amélioration (optimisation)
Le terme dénormalisation est bien souvent dévoyé.
Chris Date met les points sur les i [Date 2007b]
et mentionne quelques techniques d'amélioration (optimisation en franglais)
présentées à tort comme relevant de la dénormalisation.
(Dans ce qui suit, on parlera de tables plutôt que de relvars.)
1er exemple (comparable au 1er exemple du paragraphe 2.8).
Supposons que l'on ait à structurer une table des ventes journalières des magasins de l'entreprise
Tartempion sur une période d'une semaine. Il est d'usage de structurer cette table, appelons-la
Magasin_V, à l'aide des attributs suivants : MagId, Jour, ChiffreAffaires, la paire {MagId, Jour}
étant clé. Pour améliorer (?) les performances (principe du « tout en une seule ligne »),
certains préfèrent mettre en œuvre une table,
appelons-la Magasin_H, de clé {MagId}, telle que le chiffre d'affaires fasse l'objet d'un attribut
pour chaque jour de la semaine. En général, le terme employé pour ce changement de structure est
celui de dénormalisation, et c'est à tort, car les deux tables respectent la BCNF (et même la 5NF),
elles sont bien normalisées.
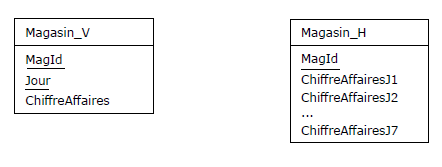
Figure 1.7 - Représentation verticale / horizontale
Maintenant, on peut faire observer que la structure de la table Magasin_H a le grave défaut de ne pas
être évolutive : si les besoins de l'entreprise deviennent décadaires, quelles seront les
conséquences ? Dans le cas la table Magasin_V, ceci sera transparent, par contre il faudra changer
la structure de la table Magasin_H, opération lourde s'il en est (sans parler des requêtes existantes
qui devront être modifiées pour prendre en compte les attributs supplémentaires).
Du point de vue de la manipulation des données, on observera que dans le cas de la table Magasin_H,
l'utilisation des opérateurs classiques d'agrégation, SUM, AVG, etc. est pour le moins
remise en question.
Du point de vue de la performance, dans les deux cas, une seule lecture d'un enregistrement physique
suffira pour connaître le chiffre d'affaires hebdomadaire d'un magasin. Mais, dans le cas de la
table Magasin_H, il serait déraisonnable d'indexer les sept colonnes si le besoin s'en faisait
sentir, en effet la performance des mises à jour est (au moins) inversement proportionnelle
au nombre d'index.
En fait, l'en-tête de la table Magasin_H ressemble plutôt à celui d'un résultat à présenter à
l'utilisateur. On doit conserver la structure de la table Magasin_V, et créer
une
vue VH afin de présenter les données selon la structure de la table Magasin_H, ça n'est
quand même pas bien sorcier. Se reporter chez DVP à
l'exemple des clients et des options.
Le mieux est encore d'en passer par un
instantané (
snapshot) rafraîchi à chaque mise à jour
(la vue « matérialisée » (oxymore...) de SQL).
2e exemple.
Supposons que la table Magasin_V ci-dessus corresponde à un regroupement de tables par régions :
Ces tables sont normalisées, elles respectent la 5NF. Pour connaître le chiffre
d'affaires national, c'est l'opérateur UNION que l'on utilisera. On peut du reste créer une
vue d'union ou un instantané pour définir la table virtuelle Magasin_V (puis la vue VH).

Figure 1.8 - Décomposition verticale
 |
A noter que, si le SGBD permet le partitionnement des tables, on pourra se contenter de n'avoir
qu'une table des magasins, en affectant une partition à chacun d'eux
(tout en définissant au besoin une vue par magasin).
|
3e exemple.
Si les magasins sont en relation avec les produits, leur chiffre d'affaires par produit peut être
géré de façon redondante : le chiffre d'affaires total par produit, est égal à la somme
des chiffres d'affaires par magasin et par produit, il y a donc redondance (avec tous les risques
d'incohérence inhérents). Mais ces deux tables respectent encore la BCNF (et la 5NF).
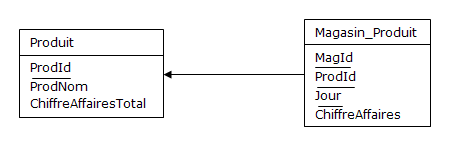
Figure 1.9 - Redondance inter-tables
N.B. Pour éviter de prendre des risques, on peut sous-traiter au SGBD le contrôle de la redondance,
en attachant à la table Magasin_Produit un trigger chargé du calcul du chiffre d'affaires total des magasins
concernés et qui mette ainsi à jour la table Produit en temps réel. Pour ne pas polluer cette table
par les mises à jour, on peut préférer déplacer l'attribut ChiffreAffairesTotal dans un instantané,
comme dans les exemples précédents.
4e exemple.
Un client passe commande. Une commande se décline en lignes de commande. Pour chaque ligne de commande,
on s'engage
en fonction des disponibilités des produits en stock, en cours de fabrication, des approvisionnements
en cours, etc. ; un engagement est composé à son tour de parties livrables en fonction du nombre
de camions nécessaires pour l'acheminement, etc.
.png)
Figure 1.10 - Identification relative et redondance intra-clés
Par référence aux RVA (cf. paragraphe 2.6), la commande représente une propriété multivaluée du client,
la ligne de commande représente à son tour une propriété multivaluée de la commande, l'engagement sur
ligne de commande une propriété multivaluée de la ligne de commande, etc.
Dans le diagramme ci-dessus, on a déplié les RVA et utilisé l'identification relative (cf. note qui suit),
source de redondances au sein des clés.
(N.B. Dans le diagramme, les clés primaires sont soulignées,
les clés étrangères sont en italiques, sachant que les attributs appartenant à une clé primaire peuvent
aussi appartenir à une clé étrangère ; les principales clés alternatives
— celles qui sont connues de l'utilisateur — sont soulignées en traits discontinus).
Note concernant l'identification relative
Revenons sur l'exemple précédent. Utiliser l'identification relative revient à considérer
(au niveau logique) que la clé d'une table — par exemple Commande — est composée des attributs
composant la clé de la table dont elle est une propriété multivaluée (Commande est une propriété
multivaluée de Client et conceptuellement parlant, il s'agit d'une entité-type faible), plus
un attribut permettant de distinguer chaque commande d'un client donné. Selon l'usage, cet
attribut supplémentaire est de type Entier et numérote chaque commande relativement à un client.
Exemple (clés soulignées) :
Client {CliId, CliNom, CliSiret, ...}
1
Dubicobit
12345678900001
2
Frichmoutz
31415926500009
...
...
...
Commande {CliId, CdeId, CdeNo, CdeDate, ...}
1
1
123456
15/02/2009
1
2
234567
01/04/2009
1
3
234575
02/04/2009
2
1
123023
20/01/2009
2
2
230239
17/03/2009
2
3
256789
06/01/2010
...
...
...
...
Du point de vue de l'utilisateur, le client Dubicobit a passé les commandes 123456, 234567 et 234575.
Du point de vue du système, les commandes <1, 1>, <1, 2> et <1, 3> sont celles du client 1,
tandis que les commandes <2, 1>, <2, 2> et <2, 3> sont celles du client 2.
Par contraste, utiliser l'identification absolue pour la table Commande (qui conceptuellement parlant
n'est plus une entité-type faible) consiste à changer la composition de la clé, en remplaçant le
couple {CliId, CdeId} par un singleton {CdeId} :
Commande {CliId, CdeId, CdeNo, CdeDate, ...}
1
1
123456
15/02/2009
1
2
234567
01/04/2009
1
3
234575
02/04/2009
2
4
123023
20/01/2009
2
5
230239
17/03/2009
2
6
256789
06/01/2010
...
...
...
...
.png)
Figure 1.11 - Identification absolue systématique
L'intérêt de l'identification relative ne saute pas aux yeux, et l'on pourrait légitimement douter
de sa pertinence, donc préférer ne pas la mettre en œuvre. Que l'identification soit absolue ou relative,
les tables Commande, LigneCde, Engagement
et Livraison respectent la cinquième forme normale, mais l'identification relative est
cause de redondance au sein des clés, ce qui n'a pas lieu quand on utilise l'identification absolue.
Toutefois, cette redondance est parfaitement contrôlée par le système grâce aux contraintes d'intégrité
référentielle déclarées. Par ailleurs, d'aucuns objectent que cette redondance est nécessairement
consommatrice de ressources (mémoire, disque...), tandis que l'utilisation de l'identification absolue
entraînerait une consommation minimale. On peut montrer qu'il n'en est rien (cf. Annexe F.1) et que la
durée de certains traitements — batchs lourds notamment — peut être réduite de façon très sensible,
voire déterminante si l'on passe à l'identification relative (cf. Annexe F.2).
Conséquence de l'identification relative sur l'organisation des requêtes SQL
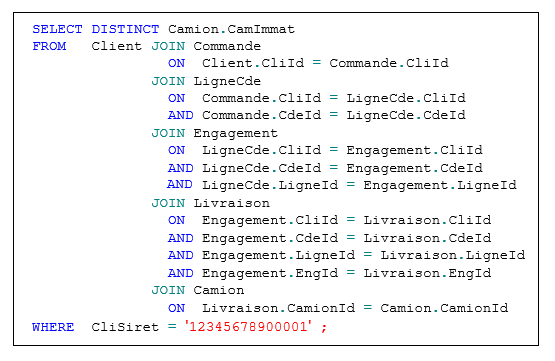
Supposons que l'on ait besoin de savoir quels camions sont concernés par les livraisons chez le
client Gillou (Siret = 12345678900001). Si on utilise l'identification absolue, on devra coder une requête SQL faisant
intervenir toutes les tables intermédiaires, à savoir Commande, LigneCde, Engagement et Livraison :
Requête 1 (identification absolue)

(Incidemment, comme on s'intéresse en particulier au client Gillou, l'opération est performante,
mais si l'on effectue des traitements de type batch, sans que les clés étrangères fassent l'objet
d'index clusters (cf. Annexes F.2 et F.3), la dégradation des performances peut poser de très gros
problèmes pour la Production informatique.)
Dans le cas de l'identification relative, on pourrait aussi écrire une requête analogue :
Requête 2 (identification relative)
Mais on peut alléger la requête ainsi :
Requête 3 (identification relative, variante)
Et plus important, on améliorera plus que substantiellement la performance en prenant un raccourci
façon couloir spatio-temporel, en codant encore plus simplement :
Requête 4 (identification relative, 2e variante)
Dans ce genre d'exercice et dans un contexte batch ou de requêtes lourdes, l'identification absolue
ne pourra évidemment pas rivaliser en performances et fera que l'on aura l'impression de faire
du surplace (cf. Annexe F.3)...
3lignes.jpg) |
Au passage, faisons observer que, grâce à la propagation de l'attribut CliId par identification relative,
de lui-même l'optimiseur de DB2 for z/OS aménage les requêtes dans lesquelles les tables intermédiaires
n'interviennent que comme courroies de transmission et les réécrit, les « optimise »
pour produire la 4e requête.
|
5e exemple.
Certains auteurs merisiens sont certes des références reconnues dans leur partie, mais ils feraient mieux de
garder le silence quand ils s'aventurent dans les terres relationnelles (Relationland), car ils sont manifestement
mal équipés pour cela. Dans [RoMo 1989], au paragraphe 6.2.6 « Optimisation du MLD relationnel »,
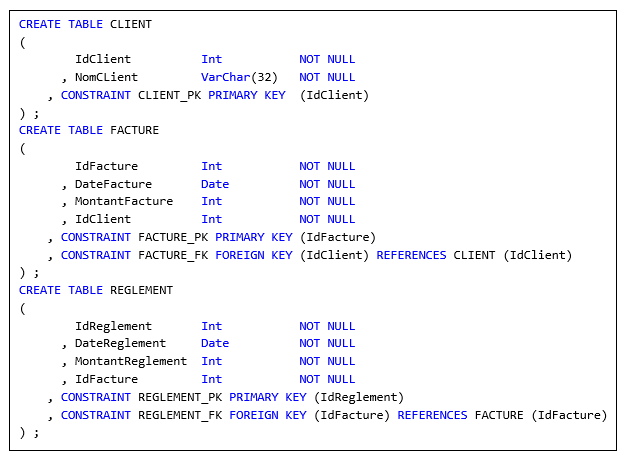
page 200, est présenté un MCD partiel d'un système de facturation, comprenant les trois entités-types suivantes :
CLIENT, FACTURE, REGLEMENT liées par des relations fonctionnelles, à savoir des CIF
(contraintes d'intégrité fonctionnelle) :

Figure 1.12 - CIF (REGLEMENT - FACTURE)
Lors du passage au MLD, est produit un ensemble de tables, dont l'équivalent reformulé en SQL peut être le
suivant (on y remplace le symbole # par Id) :
Jusque là tout va bien. Maintenant je cite (en notant que l'auteur remplace « CIF »
par « DF », mais peu importe) :
 |
« [...] La DF de REGLEMENT vers FACTURE a pour cardinalités maximales 1 dans chaque sens.
Il est indispensable de procéder à une optimisation [...]. L'optimisation présente se traduira par
l'introduction dans FACTURE de la clé étrangère #Reglement, afin de faciliter la communication
entre FACTURE et REGLEMENT. »
|
Selon l'auteur, la structure de FACTURE devrait donc impérativement
être « optimisée » ainsi :
Quelle horreur ! Je ne sais pas trop ce que l'auteur entend par « faciliter la communication »
(sic !), en tout cas on se retrouve maintenant avec un cycle entre FACTURE et REGLEMENT, outre que l'attribut
IdReglement de FACTURE doit être marqué NULL lors de la création de chaque facture, puis mis à jour
avec la valeur qui va bien à chaque règlement effectif. Cette proposition calamiteuse
d'« optimisation » est évidemment bonne pour la poubelle. Ce qu'il faut faire :
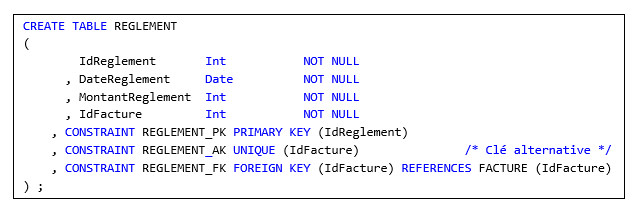
1. Ne pas toucher à la structure de la table FACTURE,
mais définir une clé alternative {Idfacture} pour la table REGLEMENT :
 |
N.B. Si nihil obstat, au niveau conceptuel identifier REGLEMENT relativement à FACTURE,
de telle sorte qu'au niveau logique l'attribut IdReglement disparaisse de REGLEMENT et que {IdFacture}
y soit à la fois clé primaire et étrangère.
|
2. Définir au besoin une vue, appelons-la FACT_RGLT, pour effectivement
« faciliter la communication », c'est-à-dire tout savoir sur les factures réglées.
Dans le style SQL, cette vue (parmi d'autres, selon les besoin) pourrait être :
Pour des raisons de symétrie, définir aussi une vue pour tout
savoir sur les factures non réglées :
Et tant qu'à faire, pour disposer d'un jeu complet,
définir une vue supplémentaire qui permette de
présenter toutes les factures, qu'elles soient notées réglées ou non réglées :
Les
tenants,
de la jointure externe de SQL
(opérateur exclu de la théorie relationnelle) préfèreront
sans doute directement coder ainsi la vue FACT_STATUT :
Mais revenons à l'étude de la normalisation, qui est quand même le sujet de cet article.
| |
| (1) |
Les mérites respectifs des logiques du premier et deuxième ordre sortent du champ de cet article.
Nous renvoyons le lecteur intéressé à l'ouvrage très didactique et non hermétique de
Willard V.O. Quine [Quine 1972], chapitre 43 « Les classes » et suivants.
Voir aussi dans l'article, le paragraphe C en annexe.
|


Copyright © 2008 - François de Sainte Marie.
Aucune reproduction, même partielle, ne peut être faite
de ce site ni de l'ensemble de son contenu : textes, documents, images, etc.
sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à
trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.


.jpg) (1) Chaque ligne représente un n-uplet de R,
(1) Chaque ligne représente un n-uplet de R,
.jpg) (2) L'ordre des lignes n'a aucune importance,
(2) L'ordre des lignes n'a aucune importance,
.jpg) (3) Toutes les lignes sont distinctes,
(3) Toutes les lignes sont distinctes,
.jpg) (4) L'ordre des colonnes est significatif —
il correspond à l'ordre S1, S2, ..., Sn des domaines sur lesquels sont définis les domaines de R.
(4) L'ordre des colonnes est significatif —
il correspond à l'ordre S1, S2, ..., Sn des domaines sur lesquels sont définis les domaines de R.
.jpg) (5) La signification de chaque colonne
est en partie rendue en l'affectant du nom du domaine correspondant. »
(5) La signification de chaque colonne
est en partie rendue en l'affectant du nom du domaine correspondant. »


non_indente.jpg)
non_indente.jpg)

.png)
non_indente.jpg)




non_indente.jpg)
non_indente.jpg)
non_indente.jpg)
non_indente.jpg)
non_indente.jpg)
non_indente.jpg)
non_indente.jpg)






.png)
.png)



3lignes.jpg)