Bases de données relationnelles et normalisation :
de la première à la sixième forme normale
Date de publication : 07/09/2008. Date de mise à jour : 14/07/2012.
2. Première forme normale
2.1. La situation en 1969
2.2. 1970 : Acte de naissance de la première forme normale
2.3. Années 1970-1980. Les théoriciens du Modèle Relationnel sont-ils en phase avec Codd ?
2.4. L'esprit et la lettre
2.5. L'atomicité : un critère absolu ?
2.6. Début des années quatre-vingt-dix. Les RVA (attributs dont les valeurs sont des relations)
2.7. Pour conclure avec la première forme normale
2.8. Le bêtisier. Les définitions non conformes de la 1NF
2. Première forme normale
Beaucoup de choses vraies ou fausses ont été dites au sujet de la première forme normale (1NF), aussi un
retour aux sources ne sera-t-il pas de trop. Rappelons une fois de plus que c'est Ted Codd qui a inventé
et théorisé le concept de normalisation pour les bases de données, et il serait malvenu de chahuter sans
raison profonde les définitions qu'il en a données. Les théoriciens du relationnel sont restés en phase
avec ce qu'a écrit Codd, tout en fournissant à l'occasion quelques précisions. Mais le Modèle Relationnel
de Données n'est pas figé pour l'éternité, il a connu et connaîtra encore bien des évolutions.
Ainsi, sans se départir de l'esprit insufflé par son inventeur, Date et Darwen ont-ils été amenés une
vingtaine d'années plus tard à approfondir la 1NF, et ce avec une extrême rigueur.
2.1. La situation en 1969
Dans son tout premier article concernant le Modèle Relationnel de Données (cf. [Codd 1969] page 2),
Codd fournissait un exemple (ici francisé) de représentation plate d'une relation de degré 4, décrivant les livraisons
de pièces par des fournisseurs, à l'usage de projets, selon certaines quantités :
.png)
Figure 2.1 - Les livraisons, représentation traditionnelle
Cette représentation tabulaire, tout à fait classique et « sage » n'appelle pas de commentaires particuliers.
Dans ce même article, Ted Codd avait écrit (page 3) :
|
« Nous avons traité de relations définies sur des domaines simples — domaines dont les éléments
sont des valeurs atomiques (non décomposables). Les valeurs non atomiques peuvent être
prises en considération dans le cadre relationnel. Ainsi, certains domaines peuvent avoir des relations
comme éléments. Ces relations peuvent à leur tour être définies sur des domaines non simples,
et ainsi de suite.
[...] L'adoption d'une perception relationnelle des données, autorise le développement d'un sous-langage
universel de recherche, basé sur le calcul des prédicats du deuxième ordre.
[...] Le calcul des prédicats du deuxième ordre est nécessaire (plutôt que celui du premier ordre)
parce que les domaines sur lesquels les relations sont définies peuvent à leur tour contenir
des éléments qui sont des relations. »
|
Et reprenant l'exemple précédent, Codd propose une représentation sous forme de relations emboîtées :
.png)
Figure 2.2 - Les livraisons, avec emboîtement de relations
Cette fois-ci, la relation P est binaire (degré 2), ses domaines sont Fournisseur (simple) et Q (non simple).
La relation emboîtée Q est à son tour binaire et ses domaines sont Pièce (simple) et R (non simple).
Les domaines de la relation emboîtée R sont tous simples.
2.2. 1970 : Acte de naissance de la première forme normale
En 1970, dans son article de loin le plus cité et considéré comme celui dans lequel sont posées
les fondations du Modèle Relationnel de Données [Codd 1970], Codd encourage à l'utilisation
de domaines simples (page 381) ce qui permet d'éliminer le problème (s'il existe) du calcul des prédicats
du deuxième ordre adopté l'année précédente :
|
« L'utilisation d'un modèle relationnel de données [...] permet de développer un sous-langage
universel basé sur le calcul des prédicats. Si la collection des relations est en forme normale,
alors un calcul des prédicats du premier ordre est suffisant. »
|
« Forme normale » étant à interpréter aujourd'hui comme « Première forme normale » (1NF).
Le concepteur de bases de données relationnelles — qu'il en soit conscient ou non — applique la
1NF à la lettre parce que les domaines des attributs de ses tables sont simples.
Même chose pour celui qui conçoit des MCD au sens Merise et qui applique la règle dite de vérification,
selon laquelle : « Dans chaque occurrence d'individu-type ou de relation-type on ne trouve qu'une seule
valeur de chaque propriété » [TRC 1989].
A noter que divers chercheurs et auteurs (par exemple [Jaeschke 1982], [Abiteboul 1984], [Korth 1988])
ont fait des propositions pour « étendre » le Modèle Relationnel et réintroduire la possibilité d'emboîter
les relations les unes dans les autres. Les systèmes dans lesquels on s'affranchit de la
première forme normale sont dits « Non première forme normale » (Non First Normal Form,
NF² en abrégé).
Il s'agit d'un sujet qui sort de notre périmètre et que nous ne traiterons pas,
d'autant plus que Date et Darwen ont montré que l'emboîtement des relations (en tant que valeurs)
était possible sans avoir à
étendre le Modèle Relationnel (cf. paragraphe 2.6).
1971 : Définition de la première forme normale
Dans son article de 1970, Codd décrit la 1re forme normale et c'est en 1971 qu'il en donne la définition
(cf. [Codd 1971], page 31) :
|
« Une relation est en première forme normale si aucun de ses domaines ne peut contenir des éléments
qui soient eux-mêmes des ensembles. Une relation qui n'est pas en première forme normale est dite non
normalisée. »
|
Ainsi, une relation (ceci vaut pour une table SQL) est en première forme normale (1NF) si aucun de ses attributs
ne peut prendre de valeur qui soit elle-même un ensemble, en l'occurrence une relation.
Selon les critères de Codd, si un SGBD acceptait l'instruction suivante, alors il autoriserait pertinemment
le viol de la 1NF. En effet, l'attribut Messages est propre à contenir des relations
(disons des tables dans un contexte SQL) :

Figure 2.3 - Viol de la 1NF
Pour rester en accord avec Codd, la structure précédente peut être transformée exactement
comme il le montre dans son article de 1970, en procédant par scissiparité, ce qui donne lieu
à deux structures, Membre et Message :
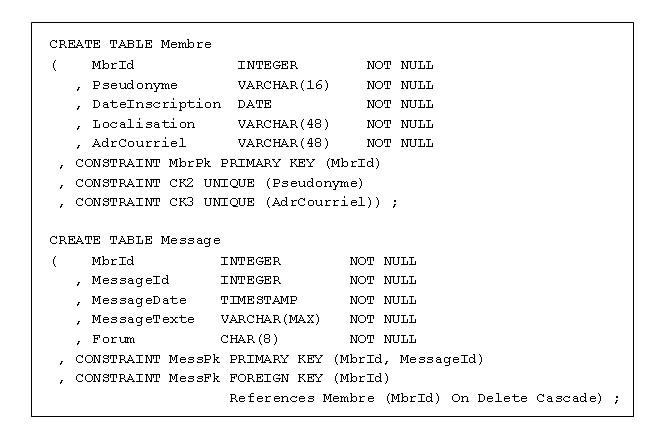
Figure 2.4 - Respect de la 1NF
(La contrainte MessFk n'est présente que pour des raisons de cohérence entre les deux tables).
2.3. Années 1970-1980. Les théoriciens du Modèle Relationnel sont-ils en phase avec Codd ?
On a brièvement noté que des auteurs comme Roth, Korth et Silberschatz proposèrent une extension
du Modèle Relationnel afin de réintroduire le principe des relations emboîtées les unes dans
les autres (relations NF²).
Mais de façon générale, les théoriciens du relationnel ont fourni dans leurs écrits des définitions
de la 1NF conformes à celle de Codd, y compris du reste ceux qui viennent d'être cités. Par exemple :
|
— « Un schéma de relation R est en première forme normale (1NF) si les domaines de l'ensemble
des attributs de R sont atomiques. Un domaine est atomique si ses éléments sont indivisibles. » [Korth 1986]
— « Une relation R est en première forme normale (1NF) si et seulement si tous les domaines
sous-jacents contiennent uniquement des valeurs atomiques. »
[Date 1986]. Plus tard, Date modifiera sa définition, cf. paragraphe 2.7.
— « Une relation est en première forme normale si tout attribut contient une valeur atomique. »
[Gardarin 1988]
— « Une relation est dite “normalisée” ou en “première forme normale” (1NF) si aucun attribut
qui la compose n'est lui-même une relation, c'est-à-dire, si tout attribut est atomique (non décomposable). »
[Miranda 1986]
|
Codd lui-même reprit le concept omniprésent d'atomicité et écrivit en 1990, dans son ultime ouvrage
de référence traitant du Modèle Relationnel de Données [Codd 1990] :
|
« The values in the domains on which each relation is defined are required to be atomic with respect
to the DBMS. »
|
D'autres considérèrent, à juste titre, que les relations sont de facto normalisées 1NF
parce qu'ils ne traitent par définition que de domaines dont les valeurs ne sont pas des ensembles
(Delobel et Adiba, Ullman, ...)
Par exemple, Jeff Ullman se contente d'écrire (cf. [Ullman 1982],
« Normal forms for relation schemes ») :
 |
« Nous n'utilisons pas de domaines dont les valeurs sont des ensembles, et nous pouvons donc
nous dispenser de mentionner la première forme normale. Nous considérons en effet que “relation”
est synonyme de “relation en première forme normale.” »
|
2.4. L'esprit et la lettre
La définition de la 1NF par Ted Codd est précise. Mais on se situe parfois à la limite quant à
son interprétation par les utilisateurs. Par exemple, le catalogue de DB2 for z/OS comporte
une table appelée SYSCOPY, utilisée pour les opérations de recovery, laquelle comporte une colonne
DSVOLSER de type VARCHAR(1784), utilisée pour stocker la liste des numéros à 6 chiffres
(séparés par des virgules) des disques hébergeant les données d'une table. L'instruction SQL
suivante est conforme du point de vue de la normalisation :
INSERT INTO SYSCOPY (..., DSVOLSER, ...)
VALUES (..., "000701,010002,...,314116", ...) ;
En effet, au sens de Codd, la chaîne de caractères "000701,010002,...,314116" est atomique, car c'est
une valeur tirée du domaine VARCHAR(1784) lequel, à la lettre, est bien atomique, en vertu de quoi
la table SYSCOPY respecte la 1NF. Évidemment, si on veut savoir quelles tables (en fait quels table spaces)
sont hébergées par le disque "314116", il suffit en SQL de coder par exemple :
SELECT DISTINCT TSNAME
FROM SYSCOPY
WHERE DSVOLSER LIKE ("%314116%") ;
Et pourtant, on pourrait discuter sans fin du bien-fondé de l'organisation de cette liste de numéros.
En tout cas, on peut examiner cet exemple à la lumière de ce qu'a écrit Serge Miranda [Miranda 1988] :
|
« Une relation est dite normalisée (ou en «première forme normale» notée 1NF) si chaque valeur
d'attribut est atomique (c'est-à-dire n'est pas un ensemble ou une liste) ; tout attribut d'une relation
1NF doit donc être monovalué. »
|
Ou du jugement sans appel de Chris Date ([Date 2007a], page 129) :
|
« Une colonne (attribut) C constitue un “groupe répétitif” si étant définie sur le domaine D,
les valeurs légales pouvant apparaître dans C sont des ensembles (ou des listes, des tableaux, ou ...)
de valeurs du domaine D. Ces groupes répétitifs sont définitivement proscrits du Modèle Relationnel. »
|
(Ne nous méprenons pas, un attribut peut faire référence à un domaine de chaînes de caractères, d'intervalles,
de polygones, de tableaux, de relations, de ce que l'on veut. Ce qui est proscrit ici est bien le caractère
répétitif des valeurs au sein d'un attribut faisant référence à un domaine (type) donné.)
En tout état de cause, la table SYSCOPY ne contrevient pas à la 1NF. Une façon d'éviter toute équivoque consisterait
à y contrevenir sciemment, comme le permet PostgreSQL, grâce aux tableaux de valeurs.
Au lieu d'écrire :
CREATE TABLE SYSCOPY
(DBNAME CHAR(8)
NOT NULL,
TSNAME CHAR(8)
NOT NULL,
...
DSVOLSER VARCHAR(1784) NOT NULL,
...) ;
Avec PostgreSQL il suffirait d'écrire, en appelant un chat un chat :
CREATE TABLE SYSCOPY
(DBNAME CHAR(8)
NOT NULL,
TSNAME CHAR(8)
NOT NULL,
...
DSVOLSER TEXT[ ]
NOT NULL,
...) ;
Puis :
INSERT INTO SYSCOPY (DBNAME, TSNAME, DSVOLSER, ...)
VALUES ("fsmrelb1", "fsmrelt1", ..., ARRAY ["000701", "010002", ..., "314116"], ...) ;
Il est quand même écrit dans la documentation de PostgreSQL :
|
« Chercher des éléments particuliers dans un tableau peut être le signe d'une mauvaise conception
de la base de données. Étudiez la mise en place d'une table séparée dont chaque ligne soit
affectée à chaque élément du tableau. La recherche sera plus simple et cela sera plus adapté si ces
éléments sont nombreux. »
|
Qui plus est, l'affectation d'une séquence à des éléments contrevient à l'esprit du Modèle Relationnel.
2.5. L'atomicité : un critère absolu ?
Revenons sur les définitions données ci-dessus de la 1NF et dans lesquelles l'accent est donc mis sur l'atomicité.
Comme l'a écrit Codd, Atomique signifie non décomposable, pour autant que
le système est concerné : si une donnée réputée atomique cache en réalité une structure complexe,
le système n'en a pas connaissance. Il en va ainsi de la colonne DSVOLSER de la table SYSCOPY,
dans laquelle se cache une liste comme nous l'avons observé précédemment.
Examinons maintenant le contenu de la table Membre de la Figure 2.4, réputée en 1NF :
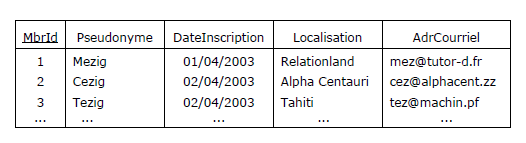
Figure 2.5 - Valeurs atomiques
A l'intersection de chaque ligne et de chaque colonne, on a exactement une valeur et celle-ci
est atomique, non décomposable en l'état par le SGBD. Ainsi, la date d'inscription d'un membre
est définie comme prenant ses valeurs dans le domaine DATE : ce domaine fait partie des domaines de
base proposés par le système, et si ce dernier n'a pas a priori la connaissance sémantique de ce que
à quoi on a accès au niveau subatomique, à savoir le jour, le mois, l'année, il met néanmoins à notre
disposition des fonctions ad hoc correspondantes, telles DAY, MONTH, YEAR.
De même, si l'on définissait une colonne
CodePostal de type CHAR(5) pour les codes postaux des communes, le système n'aurait pas la connaissance
sémantique de la structure interne de ces codes, à savoir par exemple que les deux premiers caractères
représentent le numéro du département du bureau distributeur du courrier de la commune
(les trois premiers caractères en France d'outre-mer). Cependant, le système nous permet, là encore,
d'accéder au niveau subatomique, au moyen de la fonction SUBSTRING ou du prédicat LIKE.
Observons encore que la notion d'atomicité est tout à fait relative et élastique, même si
« atomique » veut
dire : non décomposable, indivisible. Considérons par exemple la colonne MbrId, qui est du type INTEGER.
Quid si MbrId vaut 42 ? La valeur 42 est-elle atomique ? On pourrait pinailler et répondre négativement,
car 42 est décomposable en facteurs premiers : 42 = 1 X 2 X 3 X 7.
De la même façon, la chaîne de caractères
"Developpez.com" peut être considérée comme étant composée de la séquence de caractères :
"D,e,v,e,l,o,p,p,e,z,.,c,o,m". Pour ne pas s'embarquer dans la controverse on peut préférer utiliser
un autre adjectif, en remplaçant « atomique » par « scalaire »
(voire « encapsulé »,
mais ce terme est connoté Orienté Objet) signifiant que le type (domaine), la colonne, la valeur,
la variable, n'ont pas de composants directement visibles, mais accessibles, grâce à des opérateurs ad hoc,
fournis avec le type, point barre. Par contraste, l'en-tête d'une relation n'est pas scalaire,
puisque ses composants (ses attributs) sont visibles par l'utilisateur : la relation et le tuple (n-uplet)
sont à ce jour les seuls objets qui, selon la théorie relationnelle, font légalement l'objet de
types non scalaires (d'où un aménagement de la définition de la 1NF, cf. paragraphe 2.7).
En tout état de cause, les types ARRAY et MULTISET de SQL n'en font pas partie, mais pourraient
très bien être pris en compte comme cela est précisé à propos des remarques concernant Tutorial D
(cf. le paragraphe A en annexe).
2.6. Début des années quatre-vingt-dix. Les RVA (attributs dont les valeurs sont des relations)
Codd mit sa casquette de logicien quand il écrivit en 1970 qu'un calcul du premier ordre suffit pour manipuler
toutes les relations possibles, dans tous les sens et jusqu'à plus soif (autrement dit en vertu des
principes de complétude et de fermeture), alors que l'année précédente
il partait sur la base d'un calcul du deuxième ordre (cf. le paragraphe C en annexe).
L'homo relationalis aurait aimé en savoir plus sur ce revirement basé tout d'abord sur la simplicité de
la représentation des données.
Malheureusement, le père du Modèle Relationnel nous a quittés et l'on ne peut que conjecturer
quand on lit : « the possibility of eliminating nonsimple domains appears worth investigating ».
On a vu par ailleurs des gens comme Roth, Korth et Silberschatz se comporter en « hérétiques »
et proposer d'étendre le Modèle Relationnel grâce notamment à de nouveaux opérateurs (en particulier
NEST/UNNEST), permettant d'atomiser récursivement des relations NF² (Non First Normal Form), relations
dont les valeurs peuvent être des relations, à une profondeur quelconque. De leur côté, les gardiens
du phare, Date et Darwen, n'ont pas manqué eux aussi d'étudier la possibilité de manipuler des relations
contenant d'autres relations, mais tout en respectant la 1NF (aménagée).
Au début des années quatre-vingt-dix, dans un article intitulé « Relation-Valued Attributes or Will
the Real First Normal Form Please Stand Up? » [Date 1992], D & D se sont livrés
à une réflexion approfondie sur la véritable nature de la première forme normale :
|
« Nous examinons la véritable nature de la première forme normale, et avançons qu'il y a un
certain nombre d'avantages à autoriser les attributs des relations à contenir des valeurs qui soient
à leur tour (qui encapsulent) des relations. »
|
Leur constat fut — pour faire court — qu'à condition de laisser tomber la récursivité
(cf. [Date 2007a], pages 126-127) et d'en rester aux opérateurs déjà existants, on pouvait utiliser
avec profit des
RVA (
relation-valued attributes), sans avoir à étendre
le Modèle Relationnel (évolution, oui, mais révolution, non), tout en restant dans le cadre de
la première forme normale, dont la définition évolue malgré tout (cf. paragraphe 2.7),
comme on l'a déjà brièvement évoqué. Par scrupule, Date a consulté les logiciens,
mais personne n'a pu lui montrer que l'utilisation des RVA nécessitait d'en passer par
une logique du deuxième ordre (cf. [Date 2007b], page 394). En passant, insistons sur le fait que
les RVA ne contiennent que des
valeurs (relations), jamais de
variables (relvars),
ces choses que le deuxième ordre permet pour sa part de quantifier.
Pour traiter des RVA, rappelons que, outre les opérateurs de base bien connus : RESTRICT, PROJECT, JOIN
etc., D & D ont utilisé deux opérateurs faisant partie depuis une vingtaine d'années
du Modèle Relationnel (et provenant du langage relationnel ISBL, lequel date des années soixante-dix) :
RENAME et
EXTEND. On trouvera dans un article rédigé par Darwen en 2005
(«
HAVING A Blunderful Time »)
l'importance du rôle joué par ces deux opérateurs, que nous allons être amenés à utiliser
(concernant leur notation, se reporter au paragraphe B en annexe).
Exemple
Considérons les trois variables relationnelles sans prétention, qui constituent les piliers de la
base de données relationnelle « Fournisseurs et Pièces » chère à Chris Date
(base de données que nous francisons ici). La variable F est utilisée pour décrire les fournisseurs,
la variable P concerne les pièces et la variable FP des liens qui unissent fournisseurs et pièces
(« Quels fournisseurs ont livré quelles pièces »,
« Quelles pièces ont été livrées par quels fournisseurs »).
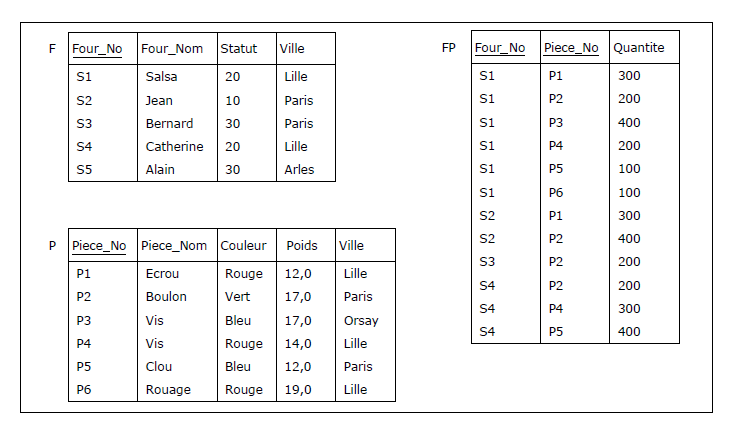
Figure 2.6 - Base de données des fournisseurs, des pièces et des livraisons
On trouve en annexe (paragraphe B), l'exemple le plus simple qui soit de l'utilisation de l'opérateur
EXTEND pour produire à partir d'une relation R une relation R′
dont l'en-tête est celui de R, augmenté d'un attribut.
Mais on peut aller beaucoup plus loin et produire une relation dont un attribut prend des valeurs
qui sont des relations. Considérons en ce sens l'expression suivante, écrite en Tutorial D,
utilisée pour présenter chaque fournisseur avec un inventaire des pièces qu'il fournit,
le résultat étant illustré à l'aide de la Figure 2.7 :

La construction
WITH <liste d'opérations> : <expression relationnelle>
permet de fournir sous forme d'une liste d'éléments séparés par des virgules, les opérations que
l'on souhaite exécuter en séquence, pour produire au final la relation définie par <expression relationnelle>.
La finalité de la liste étant de simplifier l'organisation des opérations qui, à défaut, pourraient devenir
compliquées à exprimer.
En l'occurrence, on produit d'abord une relation T1 qui ne diffère de la relation F que par le nom de l'attribut
Four_No_Bis. On procède ensuite à l'extension de T1 en récupérant dans FP l'ensemble des tuples pour lesquels
la valeur de l'attribut Four_No est égale à celle de l'attribut Four_No_Bis de la relation T1, puis en effectuant
une projection sur les attributs Piece_No et Quantite et en nommant Piece_Qte l'attribut (du type RELATION) obtenu
par extension. La relation obtenue est nommée T2. Le résultat final F_EXT est celui de T2, en renommant pour finir
Four_No_Bis en Four_No.
La représentation graphique de la relation F_EXT est la suivante :
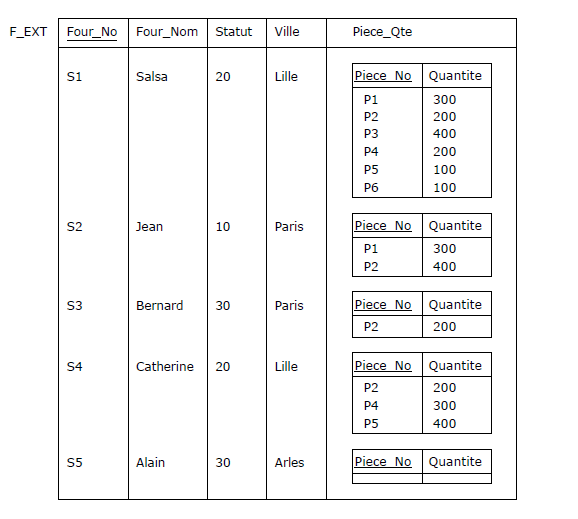
Figure 2.7 - Relation avec attribut à valeur relation (RVA)
Dans la relation F_EXT, les attributs Piece_No et Quantite ont été remplacés par le seul attribut Piece_Qte.
Les autres attributs n'ont pas changé. Chaque valeur prise par l'attribut Piece_Qte est une relation
(donc en-tête compris), une relation par attribut et par tuple de F_EXT : chaque tuple de F_EXT contient
exactement une valeur pour chacun de ses attributs et cette relation est en première forme normale
(cf. paragraphe 2.7). Noter que,
pour le fournisseur S5, le corps de la relation {Piece_No, Quantite} est l'ensemble vide {}.
En Tutorial D, on pourrait du reste définir une relvar F_EXT :
Intérêt des RVA
Une relation comme F_EXT présente des avantages indéniables :
-
Dans la Figure 2.7, le fait que le fournisseur S5 (Alain) n'a pas livré de pièces est représenté par
l'ensemble vide au sein de l'attribut Piece_Qte de la relation F_EXT, alors que — en se plaçant
dans un contexte SQL — si l'on utilisait
une jointure externe (LEFT OUTER JOIN), le résultat ci-dessous serait pollué par le bonhomme NULL et
ne pourrait même pas être doté d'une clé, en l'occurrence la paire {Four_No, Piece_No} : F_EXT ne
pourrait donc être une relation et le principe de fermeture ne serait pas respecté
(horresco referens !) :
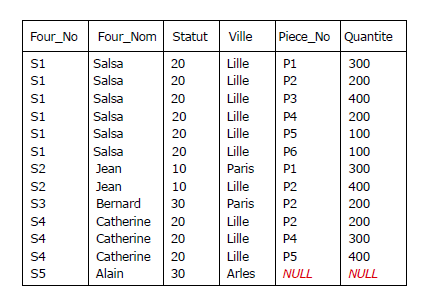
Figure 2.8 - LEFT OUTER JOIN de F et FP
-
En comparant la Figure 2.7 et la Figure 2.8, on se rend compte que dans le premier cas, la redondance est absente,
alors qu'elle foisonne dans le second cas.
-
La Figure 2.7 correspond à une relation peut-être plus proche de la vision qu'ont certains utilisateurs
(ceux pour lesquels, sémantiquement parlant, la relation FP de la Figure 2.6 est une propriété multivaluée
de la relation F, plutôt que de la relation P).
Dans leur article mentionné ci-dessus
« Relation-Valued Attributes or Will the Real First Normal Form Please Stand Up? »,
D & D fournissent nombre d'observations supplémentaires portant sur l'intérêt des RVA.
Opérateurs GROUP et UNGROUP
Notons en passant que D & D ont prévu deux opérateurs non indispensables (en effet, ce sont des combinaisons
d'autres opérateurs), mais permettant d'élever d'un cran le niveau d'abstraction (donc de nous simplifier la vie,
ainsi que celle de l'optimiseur) pour effectuer des requêtes dans lesquelles
interviennent des RVA, à savoir GROUP et UNGROUP. Ainsi, pour obtenir l'équivalent RVA de
la relvar FP de la Figure 2.6 :
La relation obtenue est représentée dans la Figure 2.9. Inversement, si FPQ désigne cette relation,
on peut lui faire subir une opération de dégroupement et retrouver FP :
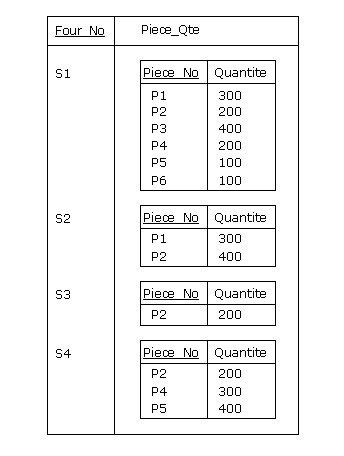
Figure 2.9 - Groupement de FP par Four_No
Inconvénients des RVA
La relation F_EXT (Figure 2.7) est la source d'un phénomène d'
asymétrie
fort gênant,
empoisonnant la vie des utilisateurs d'un SGBD hiérarchique comme IMS/DL1, avec lequel on représente
de facto les données à la manière des RVA.
Par exemple, si l'on considère les requêtes :
1. Quels fournisseurs ont livré la pièce P2 ?
2. Quels sont les pièces livrées par le fournisseur S2 ?
Dans un contexte symétrique, elles sont traduites ainsi (en Tutorial D) :
1. (FP WHERE Piece_No = Piece_No ('P2')) {Four_No}
2. (FP WHERE Four_No = Four_No ('S2')) {Piece_No}
Tandis que dans un contexte asymétrique, elles donnent lieu à celles-ci :
1. ((F_EXT UNGROUP (Piece_Qte)) WHERE Piece_No = Piece_No ('P2')) {Four_No}
2. ((F_EXT WHERE Four_No = Four_No ('S2')) UNGROUP ((Piece_Qte)) {Piece_No}
Quant aux contraintes du genre intégrité référentielle, les choses peuvent se compliquer.
Si définir une clé étrangère entre les relvars FP et P est chose simple :
FOREIGN KEY {Piece_No) REFERENCES P (Piece_No)
Entre F_EXT et P, ça l'est moins :
(F_EXT UNGROUP (Piece_Qte)) {Piece_No}
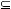
P {Piece_No}
Considérons maintenant les opérations de mise à jour. Exemple :
1. Ajouter dans la base de données le fait que
le fournisseur S5 a livré la pièce P5 en quantité 100.
2. Ajouter dans la base de données le fait que
le fournisseur S2 a livré la pièce P5 en quantité 200.
Dans un contexte symétrique, elles sont traduites ainsi :
1.
INSERT FP RELATION {TUPLE {Four_No Four_No ('S5'),
Piece_No Piece_No ('P5'),
Quantite Quantite (100)}} ;
2.
INSERT FP RELATION {TUPLE {Four_No Four_No ('S2'),
Piece_No Piece_No ('P5'),
Quantite Quantite (200)}} ;
Dans un contexte asymétrique, l'affaire se corse :
1.
INSERT F_EXT RELATION {TUPLE {Four_No Four_No ('S5'),
Piece_Qte RELATION {TUPLE {Piece_No Piece_No ('P5'),
Quantite Quantite (100)}}}} ;
2.
UPDATE F_EXT WHERE Four_No = Four_No ('S2')
(INSERT Piece_Qte RELATION {TUPLE {Piece_No Piece_No ('P5'),
Quantite Quantite (200)}}) ;
Etc.
RVA ou pas RVA ?
Si l'on se limite à l'aspect structurel des choses, les relvars « matriochkas » sont très séduisantes,
mais le phénomène d'asymétrie inhérent nous complique singulièrement la vie quand il s'agit de mettre à
jour ces relvars au moyen de l'algèbre relationnelle, ou encore d'en garantir l'intégrité. A cet égard,
quel soulagement quand, au milieu des années quatre-vingts, on put passer d'IMS/DL1 à DB2
et que l'on n'eut plus à polémiquer pour savoir si c'était l'entité-type CLIENT qui absorbait l'entité-type
CONTRAT ou inversement (bon d'accord, avec les « relations logiques » on s'en sortait, mais c'était
quand même un peu le parcours du combattant...)
2.7. Pour conclure avec la première forme normale
Si l'on reprend les définitions formelles données par Chris Date dans [Date 2004] au chapitre 6,
« Relations »,
et reprises ici en annexe (paragraphe A), le bilan concernant les relations est le suivant :
-
Tout tuple contient exactement une valeur pour chacun de ses attributs.
-
Il s'ensuit que dans chaque relation, chaque tuple contient exactement une valeur pour chacun de ses attributs.
-
Une relation qui vérifie cette propriété est dite normalisée, ou de façon équivalente, est
en première forme normale (1NF).
-
Il s'ensuit que toutes les relations en conformité avec (a) sont en 1NF.
CQFD. Si par le passé Date a donné comme tout le monde une définition de la 1NF impliquant
l'atomicité (cf. paragraphe 2.3) et donc l'illégalité des RVA, après avoir étudié la vraie nature
des types (domaines), il a été amené à remplacer la contrainte de l'atomicité par celle, moins restrictive, de
l'unicité de la valeur prise dans chaque tuple par chaque attribut : dans le contexte du Modèle Relationnel
de Données, chaque relation est ainsi de facto en 1NF.
Maintenant, une relation en 1NF est-elle pour autant parée de toutes les vertus ? L'étude des autres
formes normales (2NF et à suivre) montrera qu'il n'en est pas forcément ainsi (loin s'en faut !) et,
comme nous l'avons mentionné précédemment, on pourra être amené à couper en deux cette relation,
de manière rigoureuse, grâce aux moyens que nous ont fournis Codd, Boyce, Heath, Rissanen, Fagin,
Armstrong et autres chercheurs.
2.8. Le bêtisier. Les définitions non conformes de la 1NF
Si l'on explore le Web, on trouve des dizaines de milliers d'occurrences faisant mention de l'expression
« first normal form ». Les définitions farfelues qu'on y trouve abondent.
D'autres présentent un caractère
de sérieux certain, mais sont fausses. En voici deux exemples caractéristiques relevés dans la littérature.
Un 1er exemple
Le concept de « groupe répétitif » accompagne souvent celui d'atomicité,
et si l'on cherche sur le Web
des expressions telles que « repeating groups » ou « groupes répétitifs »,
on constate qu'il n'est pas rare qu'elles soient
incorporées dans la définition de la première forme normale, et c'est à juste titre.
Le problème est que cette fois-ci, concernant ces groupes répétitifs, on trouve couramment une
interprétation totalement différente de celle qu'en ont faite Serge Miranda, Chris Date et autres
théoriciens ou chercheurs (cf. supra, paragraphe 2.4).
A titre d'exemple, voici la définition de la 1NF selon DB2 for z/OS
(Cf. « Entity normalization » (sic !)
in DB2 Version 9.1 for z/OS, Administration Guide), définition dans laquelle l'auteur se vautre de A à Z,
je traduis :
|
« Une entité relationnelle satisfait à la contrainte de première forme normale si chaque instance d'entité
contient une seule valeur, jamais d'attributs qui se répètent. Les attributs répétitifs, souvent appelés
groupes répétitifs, sont des attributs distincts, mais il s'agit fondamentalement du même. Dans une entité
conforme à la première forme normale, chaque attribut est indépendant et unique quant à sa signification
et à son nom. »
|
A la nouvelle interprétation près de ce qu'est un groupe répétitif (ensemble d'attributs et non pas
de valeurs au sein d'un attribut), cette définition est plutôt absconse et pour être sûr d'en comprendre
le sens, il n'est pas inutile de considérer l'exemple qui l'accompagne et qui en illustre la fausseté.
En effet, l'auteur écrit, je traduis à nouveau :
|
« Supposons qu'une entité contienne les attributs suivants
EMPLOYEE_NUMBER
JANUARY_SALARY_AMOUNT, FEBRUARY_SALARY_AMOUNT, MARCH_SALARY_AMOUNT
Cette situation viole la contrainte de première forme normale, parce que JANUARY_SALARY_AMOUNT,
FEBRUARY_SALARY_AMOUNT, and MARCH_SALARY_AMOUNT sont essentiellement le même attribut,
EMPLOYEE_MONTHLY_SALARY_AMOUNT. »
|
Certes, les trois attributs mis en cause doivent passer à la trappe et sont à remplacer par le seul
attribut EMPLOYEE_MONTHLY_SALARY_AMOUNT, mais ceci relève seulement de l'art de la
modélisation conceptuelle et n'a strictement rien à voir avec la 1NF.
En effet, bien que l'auteur ait omis de préciser le domaine de référence commun aux trois attributs
prétendument peccamineux, ainsi qu'à l'attribut EMPLOYEE_MONTHLY_SALARY_AMOUNT, on peut supposer
qu'il s'agit de celui des entiers (ou des réels, peu importe),
scalaire donc (cf. paragraphe 2.5), et dans ces conditions la table EMPLOYEE_NUMBER est en 1NF.
 |
N.B. La documentation que j'ai citée et dont est tiré cet exemple mériterait d'être relue sérieusement.
Par exemple, l'expression « si chaque instance d'entité contient une seule valeur »,
peut être littéralement réécrite ainsi : « s'il n'existe pas dans la table deux lignes ayant même valeur »,
sous-entendu si une clé primaire a été définie. Bref, en plus de donner une définition fausse, l'auteur
amalgame de façon floue et absconse des concepts indépendants les uns des autres
et ne relevant aucunement de la 1NF.
(Inutile de le lui faire observer, je m'en suis chargé et j'ai même eu une réponse du Team Lead :
« I have opened a defect against this documentation and will be working with development to update
the information as soon as possible ». Ce que j'interprète volontiers ainsi :
You can always run, my little rabbit...)
|
Un 2e exemple
Il existe aussi des définitions qui peuvent conduire à des aberrations et à des contradictions.
Voici un exemple tiré d'un ouvrage dont je ne nommerai évidemment pas l'auteur (agrégé de ceci, DEA de cela, etc.),
ouvrage dans lequel on peut lire ces lignes :
|
« Un tableau est en première forme normale si toutes ses colonnes sont élémentaires et s'il
admet au moins une clef. »
|
« Tableau » est en l'occurrence synonyme de « relation » et
« élémentaire » synonyme d'« atomique ».
La 1re affirmation exprimée dans cet énoncé est correcte, mais la 2e : »s'il admet au moins une
clef » doit être évacuée ⁽¹⁾.
En effet, du point de vue du Modèle Relationnel, la nécessité
de l'existence d'une clé ne relève absolument pas de la normalisation, mais se règle en amont :
c'est une conséquence de la propriété des relations, selon laquelle celles-ci ne peuvent pas contenir
de n-uplets doublons : une relation coddienne est un ensemble fini, or un ensemble ne contient pas d'éléments en double.
A défaut, l'algèbre relationnelle fournirait des résultats faux.
On pourrait se dire : D'accord, la nécessité d'une clé ne relève pas de la normalisation, mais la définition
proposée n'est pas source de dangers. Malheureusement, sur la base de cette définition erronée,
notre clerc bien imprudent aboutit à des conclusions délirantes du genre :
|
« Un Tableau en Quatrième Forme Normale n'est pas en Troisième Forme Normale, ni même en Deuxième,
tout simplement parce qu'il n'est pas en Première Forme Normale. En effet, la condition essentielle
pour qu'un Tableau soit en Première Forme Normale est l'existence d'une Clef. »
|
En effet, il est parti de sophismes, d'énormités du genre :
|
« Il n'y a pas de Clef dans un Tableau en Quatrième Forme Normale, et celui-ci n'est donc pas
en Première Forme Normale. »
|
Et j'en passe.
La ligne jaune est franchie, notre clerc administre la preuve de sa méconnaissance des fondements mêmes
du Modèle Relationnel de Données, doublée d'une dose d'inconscience rare.
Pour faire bonne mesure, tout en oubliant de fournir la définition de la 4NF (et pour cause),
il va jusqu'à affirmer que des auteurs aussi incontestables que Delobel et Adiba seraient
les seuls à avoir démontré que celle-ci implique la BCNF, or Fagin (père de la 4NF) l'avait déjà fait en 1977.
Qui plus est, à partir de ses prémisses abracadabrantes, le clerc va jusqu'à
« prouver » que la démonstration de Delobel et Adiba (cf. paragraphe 4.14 ci-dessous)
« ne démontre rien »...
Mais on peut supposer que, si d'aventure, ces éminents chercheurs ont parcouru la prose les mettant en question,
ils l'auront fait « d'un derrière distrait » comme disait Flaubert...
_______________________________________
(1)
Curieusement, des auteurs bien connus des cercles merisiens incorporent eux aussi à la définition de la 1NF
la nécessité de l'existence d'une clé. Citons [Morejon 1992] :
« Une relation est en 1NF si :
— elle possède une clé
— tous ses attributs sont atomiques. »
Ou encore [RoMo 1989] qui tricote allègrement concepts merisiens et relationnels (page 82 de l'ouvrage) :
« Pour répondre à la 1FN tout individu doit posséder un identifiant. »


Copyright © 2008 - François de Sainte Marie.
Aucune reproduction, même partielle, ne peut être faite
de ce site ni de l'ensemble de son contenu : textes, documents, images, etc.
sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à
trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.

.png)
.png)











 P {Piece_No}
P {Piece_No}
