Bases de données relationnelles et normalisation :
de la première à la sixième forme normale

Date de publication : 07/09/2008. Date de mise à jour : 14/07/2012.

Version PDF

3. Forme normale de Boyce-Codd, deuxième et troisième formes normales
3.1. Les états d'âme provoqués par la première forme normale
3.1.1. Une tentative de normalisation en 1NF
3.1.2. Conséquences de la normalisation : des redondances à profusion
3.1.3. Les difficultés de mise à jour (Insert, Delete, Update)
3.1.4. Quelle alternative ?
3.1.5. Approche conceptuelle de la solution
3.2. L'approche analytique, ses outils
3.2.1. Remarque préliminaire
3.2.2. Dépendance fonctionnelle (DF)
3.2.3. Clé candidate
3.2.4. Surclé
3.2.5. Sous-clé
3.2.6. Clé primaire
3.3. Forme normale de Boyce-Codd (BCNF)
3.3.1. Énoncé de la BCNF
3.3.2. Théorème de Heath
3.3.3. Comment normaliser une relvar qui n'est pas en BCNF
3.3.4. Décomposition par projection - jointure préservant l'information
3.3.5. Normalisation et intégrité référentielle
3.3.6. Conséquences de la normalisation par projection - jointure
3.4. Deuxième et troisième formes normales
3.4.1. BCNF versus 2NF et 3NF
3.4.2. Deuxième forme normale (2NF)
3.5. Dépendance transitive, dépendance directe
3.6. Troisième forme normale (3NF)
3.7. Un problème embarrassant de BCNF
3.8. Retour sur la dénormalisation a priori
3.9. Une relvar respectant la BCNF peut-elle violer la 3NF ?

3. Forme normale de Boyce-Codd, deuxième et troisième formes normales

3.1. Les états d'âme provoqués par la première forme normale

3.1.1. Une tentative de normalisation en 1NF

Considérons à nouveau la table Membre de la Figure 2.3, qui pourrait représenter une ébauche de la table des membres de DVP. Au sens de Codd, cette table n'est pas normalisée en 1NF et pour la conserver sans la casser en deux, tout en normalisant, on pourrait la structurer ainsi (certains noms d'attributs ont été modifiés, pour des contraintes de représentation graphique) :

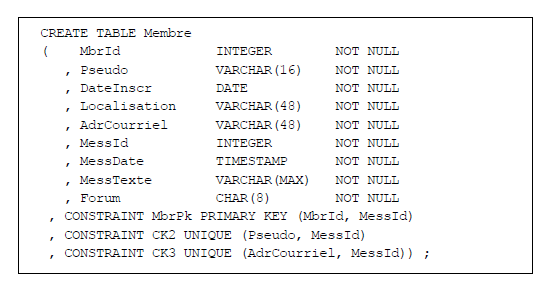
Figure 3.1 - Table Membre, normalisée en 1NF

On notera au passage qu'il a fallu faire évoluer la composition des contraintes MbrPk, CK2 et CK3. La clé primaire de la table est désormais composée de la paire {MbrId, MessId} (attributs soulignés ci-dessous).

Figure 3.2 - Table Membre, normalisée en 1NF (corps de la table)

3.1.2. Conséquences de la normalisation : des redondances à profusion

Au vu du contenu de la table de la Figure 3.2, on peut constater la présence de redondances (en rouge) ne faisant que polluer la table. On apprend ainsi quatre fois — c'est-à-dire autant de fois qu'il a échangé des messages — que le membre 31411 a pour pseudonyme fsmrel, qu'il s'est inscrit le 08/09/2006, qu'il vit dans le Relationland et qu'il a pour adresse fsmrel@xxx.re. Pour sa part, Marc en est à 20 000 messages : la normalisation en 1NF de la table Membre a provoqué une inflation déraisonnable de redondances, faisant que la table prend de l'embonpoint.

Exemple :

Coût du stockage (DB2 for z/OS V8). Par référence aux tables telles qu'elles sont décrites dans les figures 2.4 et 3.1, et sur la base d'un taux de compression d'environ 75% pour la table Membre et de 90% pour les autres tables, le coût du stockage est de l'ordre de celui-ci (en notant que dans le cas du couple de tables {Membre, Message}, l'index primaire de la table Message, de clé {MbrId, MessageId} sert aussi pour la clé étrangère {MbrId}) :

Coûts de stockage (DB2)

Contrairement à ce que l'intuition pourrait faire croire, dans le cas de la table unique (figure 3.1), le coût de stockage est supérieur à celui des tables Membre + Message de la figure 2.4.

On peut s'interroger sur le nombre de lectures/écritures en cache ou sur disque nécessaires pour, par exemple, modifier la localisation ou l'adresse de courriel de quelqu'un qui, comme Marc, a rédigé 20 000 messages. Dans le cas de l'adresse de courriel, ne pas oublier que ces lectures/écritures concernent aussi l'index utilisé pour garantir l'unicité des couples {MbrId, AdrCourriel}. Sans oublier non plus les désorganisations qui s'ensuivent, l'encombrement des fichiers journaux, les contentions entre transactions concurrentes, etc.

Tout cela, indépendamment d'une catégorie de problèmes bien connus de mise à jour, inhérents à la non normalisation, très tôt pointés par Codd et repris par tous les auteurs, problèmes évoqués dans le paragraphe 3.1.3 qui suit.

Quant aux performances concernant la lecture, si avec la table unique on évite une jointure, un prototypage en ce sens et des mesures poussées pourraient bien montrer qu'à part quelques requêtes pour lesquelles on ferait des économies (de bouts de chandelle à dire vrai), certains coûts sont cachés et peuvent être élevés (tris déclenchés par l'emploi de la clause SQL DISTINCT, etc.) sans compter que le nombre de certains niveaux d'index augmente. Se reporter au paragraphe 3.8 pour juger de prétendus méfaits dont certains accusent bien à tort la jointure, sans avoir vérifié.

Ce qui se passe réellement dans la soute n'a pas grand-chose à voir avec ce que l'on peut imaginer du haut de la dunette...

3.1.3. Les difficultés de mise à jour (Insert, Delete, Update)

L'organisation de la table Membre (Figure 3.1) pose quelques problèmes concernant les mises à jour.

Insert : On ne peut pas prendre en compte l'inscription des membres tant qu'ils n'ont pas envoyé un premier message (intégrité d'entité oblige, cf. paragraphe 3.2.6 : l'attribut MessId participe à la clé primaire et ne peut être marqué « NULL »).

Delete : Si l'on veut supprimer les messages de fsmrel, on est carrément obligé de supprimer ce dernier (intégrité d'entité oblige encore).

Update : Suite à l'exécution d'une requête mal codée, rien n'empêche de modifier le pseudonyme d'un membre seulement dans certaines lignes qui le concernent et « d'oublier » de le faire dans d'autres lignes. Bien sûr, à coups de contraintes (triggers SQL en général), on peut contrôler qu'un membre n'a qu'un pseudonyme, qu'une date d'inscription, etc. Mais quelle surcharge de travail pour le développeur et le DBA, et quel surcoût en matière de consommation de ressources pour le SGBD chargé de garantir les contraintes...

3.1.4. Quelle alternative ?

Que faire ? Se résigner à mettre en oeuvre la table Membre (Figure 3.1) respectant la 1NF ? Revenir à la situation initiale, en conservant une structure calquée sur celle de la relation de la Figure 2.3 ? Encore faudrait-il que le SGBD accepte les attributs à valeurs relations (RVA). Évidemment, aux difficultés près posées par ce genre d'attributs (cf. paragraphe 2.6), les redondances disparaissent et la table subit une sérieuse et bénéfique cure d'amaigrissement ; désormais (grâce à l'ensemble vide) une inscription peut être effectuée sans qu'il soit besoin d'attendre que le nouvel inscrit (rismo) ait envoyé son premier message ; de même, on peut supprimer tous les messages de Marc (sitôt dit, sitôt fait) sans que celui-ci disparaisse pour autant, etc., suite à quoi la table aurait l'allure suivante (structure et valeur) :

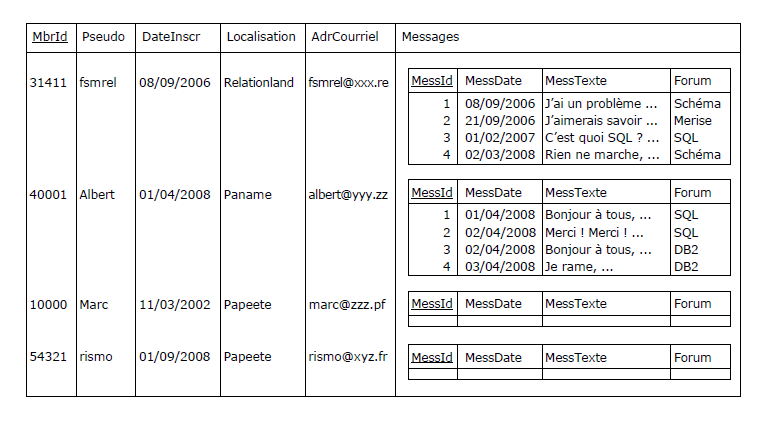
Figure 3.3 - Table Membre, avec l'attribut Messages dans une configuration RVA

3.1.5. Approche conceptuelle de la solution

Il y a bien sûr une alternative. Celui qui a l'habitude de pratiquer l'art de la modélisation conceptuelle, qu'il s'agisse de produire des MCD ou des diagrammes de classes, n'hésitera guère et fournira un diagramme qui, par dérivation, donnera lieu à des tables normalisées en 1NF, mais dépourvues d'attributs RVA, ce qui tombe à pic quand le SGBD ne permet pas la mise en oeuvre de tels attributs. Disons que l'on procède en l'occurrence selon une démarche dite synthétique, tandis que dans une étape suivante, on vérifiera la qualité du résultat, selon une démarche dite analytique, mettant en jeu les techniques de normalisation qui permettront de s'assurer que l'architecture de la base de données est valide, une fois éliminées les redondances. En fait, on pourra toujours améliorer cette architecture pour éviter par exemple la présence du bonhomme NULL, ou pour anticiper quant à la performance des applications, mais ceci sort du cadre de la normalisation. Quoi qu'il en soit, le concepteur modélisera quelque chose comme ceci :

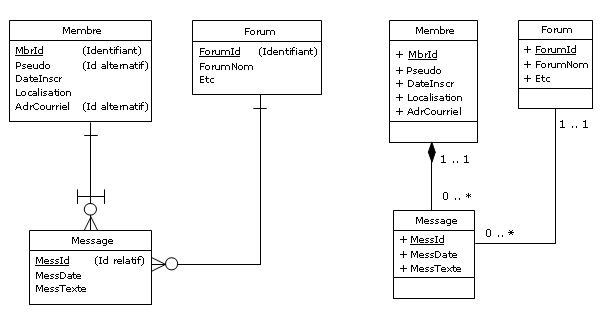
Figure 3.4 - Membres des forums - vision conceptuelle

Ce qui donnera lors de l'étape de dérivation un diagramme logique tel que celui-ci :

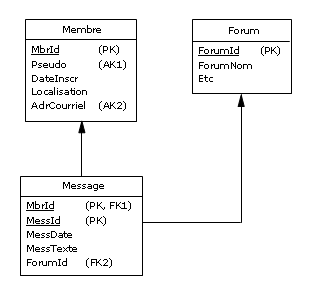
Figure 3.5 - Membres des forums - diagramme logique

Autrement dit, lors de la génération du code SQL correspondant, on retrouvera la structure des tables Membre et Message de la Figure 2.4. Vous me direz : que de détours pour revenir en quelque sorte à la case Départ ! Mais il fallait bien voir qu'il y a plus d'une façon de modéliser avant de décider d'une stratégie. Et si l'on opte pour les structures des tables de la Figure 2.4, il ne restera plus qu'à démontrer qu'elles sont en cinquième forme normale — vaste programme, mais réalisable sans grand effort dans le cas de cet exemple, grâce aux théorèmes de Date et Fagin (cf. paragraphe 5.8) :

Si une relvar est en 3NF et si chacune de ses clés candidates ne comporte qu'un seul attribut, alors cette relvar est en 5NF.

Si une relvar est en BCNF et comporte au moins un attribut non-clé, alors cette relvar est en 5NF.

3.2. L'approche analytique, ses outils

3.2.1. Remarque préliminaire

Notre défi est donc de produire une structure de base de données qui soit valide, évolutive, manipulable, c'est-à-dire débarrassée des redondances dénoncées précédemment. La théorie relationnelle nous en donne les moyens. Elle met à notre disposition des outils dont je cite certains : dépendance fonctionnelle, dépendance multivaluée, dépendance de jointure, clé candidate, surclé, théorème de Heath, théorème de Fagin-Date, opérateurs de projection et de jointure (naturelle), axiomes d'Armstrong. Grâce à ces outils on pourra s'assurer que les tables sont normalisées en 2NF, 3NF, etc. Et par une pratique synthético-analytique rappelant l'art du yoyo, on vérifiera la modélisation conceptuelle en conséquence.

Je propose ici de décrire les outils les plus indispensables, en commençant par les plus simples et qui permettent de s'assurer qu'une table est en forme normale de Boyce-Codd (BCNF), à savoir les dépendances fonctionnelles. Par ailleurs, chronologie oblige, il est d'usage de commencer par étudier la 2NF et la 3NF avant de passer à la BCNF : je procèderai néanmoins dans l'ordre inverse, car la 2NF et la 3NF ne présentent plus guère aujourd'hui d'intérêt qu'historique.

A noter que j'utiliserai ici la terminologie du Modèle Relationnel plutôt que celle du Modèle SQL, mais il est facile de traduire, en remplaçant relvar et relation par table, tuple par ligne, etc.

3.2.2. Dépendance fonctionnelle (DF)

Il est un concept capital sans lequel nous ne pourrions pas traiter de la normalisation, car non seulement il est impliqué systématiquement dans les énoncés des formes normales, mais en outre, il représente un puissant outil pour normaliser les relations : il s'agit de la dépendance fonctionnelle. C'est en quelque sorte notre rasoir d'Ockham.

_{(Guillaume d'Ockham (ou d'Occam), moine anglais du XIVe siècle,
à qui l'on doit ce sage conseil de
parcimonie :}_{Pluralitas non est ponenda sine necessitate}_{,
que nous pouvons interpréter ici comme :}_{Ne multipliez pas les redondances au-delà du nécessaire}_).

Une dépendance fonctionnelle (DF) est une instruction de la forme :

X ➔ Y

où X et Y sont deux sous-ensembles d'attributs de l'en-tête d'une relvar R, et satisfaisant à la règle : pour une valeur de X, correspond exactement une valeur de Y, c'est-à-dire que si deux tuples ont la même valeur v_x pour X, alors ils ont aussi la même valeur v_y pour Y.

On dit encore que Y est fonctionnellement dépendant de X. X est appelé le déterminant de la DF et Y le dépendant.

Pour signifier que X ne détermine pas Y, on peut écrire : X

Y.

Considérons par exemple la relvar FPV, extension de la relvar FP décrite dans la Figure 2.6 et dont l'en-tête est enrichi, juste pour les besoins de la cause, d'un attribut Ville, utilisé pour savoir dans quelle ville est localisé un fournisseur :

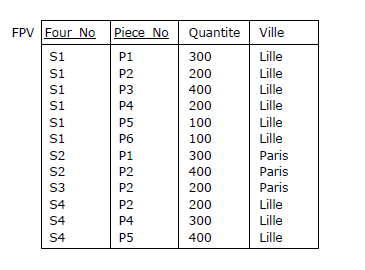
Figure 3.6 - Relvar des liens fournisseurs - pièces (enrichie de l'attribut Ville)

La relvar FPV vérifie un certain nombre de DF. Ainsi, pour signifier qu'un fournisseur est localisé dans une et une seule ville, on écrit :

    {Four_No} ➔ {Ville}

La paire {Four_No, Piece_No} étant clé candidate (cf. paragraphe 3.2.3), on a aussi les DF suivantes (entre autres) :

    {Four_No, Piece_No} ➔ {Quantite}

    {Four_No, Piece_No} ➔ {Ville}

(L'utilisation des accolades est là pour rappeler que le déterminant et le dépendant d'une DF ne sont pas des attributs, mais des ensembles d'attributs, au sens de la théorie des ensembles).

Avant de poursuivre, procédons à une classification des dépendances fonctionnelles :

Dépendance fonctionnelle triviale

SoitR une relvar et X et Y deux sous-ensembles quelconques d'attributs de l'en-tête de R. La dépendance fonctionnelle X ➔ Y est dite trivialesi Y est inclus dans X (inclusion au sens large).

La relvar FPV comporte donc (entre autres) les dépendances triviales suivantes :

    {Four_No} ➔ {Four_No}

    {Four_No, Piece_No} ➔ {Four_No}

    {Four_No, Piece_No} ➔ {Piece_No}

    {Ville, Quantite} ➔ {Ville}

    Etc.

Malgréson caractère ... trivial, la DF triviale est importante, car elle fait l'objet du1er axiome d'Armstrong (cf. paragraphe E en annexe), et elle intervient dans l'énoncé de laBCNF.
Dépendance fonctionnelle partielle

SoitR une relvar, X un sous-ensemble quelconque d'attributs de R et C un attribut quelconque de R. Ladépendance fonctionnelle X ➔ {C} est dite partiellesi elle n'est pas triviale et s'il existe Y strictement inclus dans X tel que Y ➔ {C}.

Ainsi, la relvar FPV comporte la dépendance fonctionnelle non triviale

{Four_No, Piece_No} ➔ {Ville}

laquelle est partielle, car il existe par ailleurs la dépendance fonctionnelle

{Four_No} ➔ {Ville}

Ce type de DF intervient dans l'étude de la 2NF.
Dépendance fonctionnelle irréductible à gauche (ou élémentaire ou totale)

SoitR une relvar, X un sous-ensemble quelconque d'attributs de R et C un attribut quelconque de R. La dépendance fonctionnelle X ➔ {C}est dite irréductible à gauche (ou encore élémentaire ou totale) si elle n'estni triviale ni partielle, c'est-à-dire s'il n'existe pas Y strictement inclus dans X tel que Y ➔ {C}.

Ainsi, la relvar FPV comporte la dépendance fonctionnelle irréductible à gauche

{Four_No, Piece_No} ➔ {Quantite}

Eneffet, une quantité de pièces n'a de sens que pour un fournisseur et un type de pièce donnés : pour un fournisseuron peut avoir différentes quantités de pièces et il n'existe donc pas de DF {Four_No} ➔ {Quantite}. De la même façon, il n'existe pasde DF {Piece_No} ➔ {Quantite}.

Autreexemple : au paragraphe E.6.2 en annexe, on montre qu'étant données la relvar R{A, B, C, D}et l'ensemble de DF : {{A} ➔ {B,C}, {B} ➔ {C}, {A} ➔ {B}, {A,B} ➔ {C}, {A,C} ➔ {D}}, la DF {A,C} ➔ {D} estréductible.

Ce type de DF intervient essentiellement dans l'étude de la 2NF (et dans telle ou telle définition de la BCNF).

L'expression dépendance fonctionnelle totale est celle utilisée par Ted Codd : full functional dependence [Codd 1971]. L'expression dépendance fonctionnelle irréductible à gauche (left-irreducible functional dependence) apparaît chez Date dans la 6e édition de An Introduction to Database Systems. Le qualificatif irréductible à gauche est plus précis que celui de totale (et d'élémentaire) et fait intervenir, à juste titre, la fermeture d'un ensemble de DF (cf. paragraphes E.1 et E.6.2 en annexe).

3.2.3. Clé candidate

(En notant qu'en vertu de la propriété d'unicité, la DF : K ➔ {A} est vérifiée pour chaque attribut A de R.)

Ainsi, le sous-ensemble défini par la paire {Four_No, Piece_No} est une clé candidate de la relvar FPV (clé, pour faire court). Considérons en effet les DF vues précédemment :

    {Four_No, Piece_No} ➔ {Four_No}         (DF triviale)

    {Four_No, Piece_No} ➔{Piece_No}         (DF triviale)

    {Four_No, Piece_No} ➔ {Quantite}         (DF irréductible à gauche)

    {Four_No, Piece_No} ➔ {Ville}               (DF partielle)

Du fait de ces DF, on constate tout d'abord que la paire {Four_No, Piece_No} détermine fonctionnellement chaque attribut de FPV, ce qui répond à la règle d'unicité.

Ensuite, cette paire n'est pas réductible. En effet, les sous-ensembles {Four_No} et {Piece_No} qui la composent ne sont pas assujettis, pris isolément, à respecter la contrainte d'unicité (de fait, le fournisseur S1 apparaît légalement dans 6 tuples de la relvar FPV et la pièce P2 dans 4 tuples) et ne peuvent donc pas faire à eux seuls l'objet de clés candidates.

Puisqu'elle satisfait aux contraintes d'unicité et d'irréductibilité, la paire {Four_No, Piece_No} est clé candidate.

Les triplets {Four_No, Piece_No, Quantite} et {Four_No, Piece_No, Ville} garantissent la règle d'unicité, mais sont réductibles car le sous-ensemble {Four_No, Piece_No} inclus dans chacun d'eux garantit aussi la règle : ces triplets ne peuvent être clés candidates, pas plus que le quadruplet {Four_No, Piece_No, Quantite, Ville} réductible lui aussi.

On observera qu'une relvar peut posséder plus d'une clé candidate. C'est le cas par exemple de la table Membre telle qu'elle est décrite dans la Figure 2.4 et dans sa version obèse (Figure 3.1), où la table est dotée des trois clés suivantes : {MbrId, MessId}, {Pseudo, MessId}, {AdrCourriel, MessId}.

3.2.4. Surclé

Le concept de surclé intervient souvent dans la théorie de la normalisation, il est donc important d'en donner la définition. La surclé est un surtype de la clé candidate :

La paire {Four_No, Piece_No}, les triplets {Four_No, Piece_No, Quantité}, {Four_No, Piece_No, Ville} et le quadruplet {Four_No, Piece_No, Quantité, Ville} constituent autant de surclés pour FPV.

On retiendra donc que :

Un sous-ensemble K d'une relvar R est une surclé de R si et seulement si chaque attribut C de R en dépend fonctionnellement (trivialement, partiellement ou totalement).
Une clé candidate est une surclé spécialisée, car elle est astreinte à respecter le principe d'irréductibilité outre celui d'unicité.

3.2.5. Sous-clé

Une sous-clé est un sous-ensemble (non strict) d'une clé candidate.

La paire {Four_No, Piece_No} et les singletons {Four_No} et {Piece_No} sont des sous-clés de la relvar FPV. Même chose pour l'ensemble vide {}.

On peut noter qu'une clé candidate est à la fois surclé et sous-clé.

3.2.6. Clé primaire

Dans le contexte du Modèle Relationnel lui-même, le concept de clé primaire est aujourd'hui obsolète (rasoir d'Ockham oblige). Mais du point de vue SQL, il est toujours bien présent : dans ces conditions, si une table T possède plusieurs clés candidates, on en privilégie une pour être primaire, et si T ne possède qu'une seule clé candidate, celle-ci l'est de facto. L'intention est non seulement d'« identifier » chaque tuple de T, mais aussi d'établir des ponts entre T et d'autres tables, garantir l'intégrité référentielle par le jeu des liens entre clés primaires et étrangères [Codd 1970]. Les clés candidates non retenues sont dites alternatives ou alternées, de rechange... (Alternate keys).

Avec SQL donc, même si cela est a priori arbitraire, il faut faire appel à quelques critères aidant à fixer son choix :

./images/Carre_noir(puce)non_indente.jpg

Il est impératif qu'une clé primaire soit stable, c'est-à-dire qu'elle ne change jamais de valeur. En effet, du fait des contraintes référentielles impliquant clés primaires et étrangères, le remplacement d'une valeur de clé primaire peut déclencher une cascade de remplacements de valeurs de clés primaires/étrangères dans de nombreuses autres tables et finir par pénaliser très sensiblement l'activité d'une production informatique (accès physiques aux données, phénomènes de blocage, désorganisation des données au niveau physique, etc., et n'oublions pas que pour la majorité des SGBDR, la structure d'un tuple induit celle d'un enregistrement physique, hélas !)

Par exemple, si la table des fournisseurs comporte le numéro de SIREN en tant qu'attribut, il faut éviter de faire participer celui-ci à clé primaire de la table. En effet, ce numéro est attribué par l'INSEE qui, tous les mois, fournit la liste des numéros erronés et à remplacer. Plus généralement, il ne faut pas utiliser des informations dont les valeurs sont fournies par un organisme extérieur à l'entreprise et susceptibles de changer, à l'instar de ces numéros.

De la même façon, il faut éviter d'utiliser pour les clés primaires des données dont les valeurs sont significatives, du genre : les deux premiers caractères représentent telle information, les trois suivants telle autre information, cela relativement aux deux premiers... Sinon, on en arrive à figer un système qui pourtant doit s'adapter aux évolutions propres à l'entreprise ou imposées par un système externe (l'ISBN codifié par l'ISO, l'EAN13 ou l'EAN8, les codes bancaires présents sur la ligne CMC7 des chèques, etc.)

Ainsi, une clé primaire ne doit pas pouvoir changer de valeur et ne doit donc pas être significative : elle doit être définie en accord avec l'administrateur de la base de données, lequel aura à terme le bébé sur les bras. En général, on en vient à définir un attribut artificiel de type entier, que l'on incrémente ou que l'on hache (tâches confiées généralement au SGBDR), ou encore de type TIMESTAMP, etc.

Pour des raisons de lisibilité et ne pas décourager le lecteur, nous dérogerons à cette règle en ce qui concerne certains exemples qui émaillent cet article, cf. par exemple le paragraphe 3.7, mais dans un contexte de production, on ne déroge pas).

Une clé primaire doit respecter l'intégrité d'entité au sens de Codd, c'est-à-dire qu'aucun de ses composants ne peut être marqué « NULL ».

Il est évident que si aucune clé candidate ne répond aux critères que l'on vient d'énumérer, alors il faudra inventer de toutes pièces une clé primaire qui soit conforme, en définissant à cet effet un attribut parfaitement artificiel. Ceci est à rapprocher de ce qu'a écrit Yves Tabourier au sujet des propriétés des entités-types (ou individus-types) [Tabourier 1986] page 80 :

« ... la fonction d'une propriété est de décrire les objets (et les rencontres), alors que l'identifiant ne décrit rien. Son rôle fondamental est d'être sûr de distinguer deux jumeaux parfaits, malgré des descriptions identiques.
L'expérience montre d'ailleurs que l'usage des « identifiants significatifs » (ou « codes significatifs ») a pu provoquer des dégâts tellement coûteux que la sagesse est d'éviter avec le plus grand soin de construire des identifiants décrivant les objets ou, pis encore, leurs liens avec d'autres objets... »

On ne saurait mieux dire.

Observations concernant les clés primaires

Pour leur part, les continuateurs de l'oeuvre de Codd, à savoir Date & Darwen, estiment que le choix d'une clé candidate pour être clé primaire, relève de considérations d'ordre purement psychologiques car, en quelque sorte, « elle serait plus égale que les autres ». Reste son rôle en relation avec l'intégrité référentielle : que ce soit dans le cadre du Modèle Relationnel ou du Modèle SQL, une clé étrangère pouvant être en relation avec n'importe quelle clé candidate servant de référence, on pourrait simplement exiger que la clé référencée vérifie les critères précédemment énoncés (stabilité, absence de signification, marquage « NULL » interdit). Une réflexion attentive montre qu'il faut se rendre aux arguments développés par D & D dans [Date 1995] : les deux concepts de clé primaire et de clé alternative peuvent être évacués sans rien remettre en cause au plan fonctionnel. C'est pourquoi Tutorial D (le langage de D & D) les ignore, au bénéfice du seul concept de clé (sous-entendu candidate). Mais, dans le contexte de la modélisation, il peut être utile de raisonner en termes de clé primaire (comme interprétation de l'identifiant d'une entité-type d'un modèle conceptuel de données).

Les concepts de clé primaire et de clé alternative pourraient donc théoriquement être évacués de SQL, au bénéfice du seul concept de clé (toujours sous-entendu candidate), mais il y a malgré tout la réalité des bases de données en production, et l'on ne peut donc pas supprimer du langage un mot-clé omniprésent, simplement en claquant des doigts.

3.3. Forme normale de Boyce-Codd (BCNF)

On a besoin de techniques permettant d'évacuer les anomalies de mise à jour (cf. paragraphe 3.1.3), en décomposant une relvar R en d'autres relvars R1, R2, ..., Rn, elles-mêmes dépourvues de ces anomalies. Décomposer signifie, réciprocité oblige, savoir recomposer R. Pour cela, on met en oeuvre un procédé de normalisation, s'appuyant fondamentalement sur les relations qu'il peut y avoir entre clés et dépendances fonctionnelles.

Il faut d'abord être en mesure de vérifier si une relvar est à décomposer. L'énoncé fondamental permettant de s'en assurer porte le nom de forme normale de Boyce-Codd (BCNF pour Boyce-Codd Normal Form), cf. [Fagin 1977], [Ullman 1982], [Date 2008].

3.3.1. Énoncé de la BCNF

Énoncé de Boyce et Codd [Codd 1974], où la BCNF est encore nommée 3NF :

A relation R is in third normal form if it is in first normal form and, for every attribute, collection C of R, if any attribute not in C is functionally dependent on C, then all attributes in R are functionally dependent on C.

Énoncé de Date ([Date 2008]), plus au goût du jour que le précédent, je traduis :

Une relvar R est en forme normale de Boyce-Codd (BCNF) si et seulement si pour chaque dépendance fonctionnelle non triviale A ➔ B qui doit être vérifiée par R, A est une surclé de R.

(A et B sont des sous-ensembles d'attributs de l'en-tête de la relvar R).

Variante 1, due à Carlo Zaniolo (cf. [Date 2004]) :

Soit R une relvar, X un sous-ensemble d'attributs de l'en-tête de R et A un attribut de cet en-tête. R est en forme normale de Boyce-Codd (BCNF) si et seulement si, pour chaque dépendance fonctionnelle X ➔ {A} qui doit être vérifiée par R, au moins une des conditions suivantes est satisfaite :

1. A est un élément de X (cette dépendance fonctionnelle est donc triviale).

2. X est une surclé de R.

On peut ainsi affirmer que la relvar FPV (cf. Figure 3.6) n'est pas en forme normale de Boyce-Codd, puisqu'il existe la dépendance fonctionnelle non triviale :

{Four_No} ➔ {Ville}

dont le déterminant {Four_No} ne constitue pas une surclé, car ne respectant pas la contrainte d'unicité (cf. paragraphe 3.2.3). Pour normaliser la relvar FPV, on se servira du théorème de Heath (voir ci-dessous).

Petit problème en passant: pour prouver qu'une relvar R est en BCNF il faut d'abord dresser l'inventaire complet des DF non triviales satisfaites par R, etvérifier que chacune d'elles est une surclé. Or, une DF est de la forme A ➔ B, A etB étant des sous-ensembles des attributs de R. Comme à un ensemble de n éléments correspond 2ⁿ sous-ensembles (en tenant compte de l'ensemble vide), la limite supérieure du nombre deDF est égale à 2²ⁿ.
Certains chiffres découragent...

Heureusement,on dispose d'un algorithme permettant de s'assurer relativement rapidement du respect de la BCNF (cf. paragraphe E.5 en annexe).

Variante 2 de l'énoncé de la BCNF (basée sur les dépendances fonctionnelles irréductibles à gauche) :

Soit R une relvar, X un sous-ensemble d'attributs de l'en-tête de R et A un attribut de cet en-tête. R est en forme normale de Boyce-Codd (BCNF) si et seulement si, pour chaque dépendance fonctionnelle X ➔ {A} qui doit être vérifiée par R, une des conditions suivantes est satisfaite :

1. Cette dépendance fonctionnelle est triviale (A est un élément de X).

2. Cette dépendance fonctionnelle est irréductible à gauche et X est une clé candidate de R.

Petite consolation concernant la chasse aux DF : La recherche peut être limitée aux DF irréductibles à gauche. Il n'en demeure pas moins que la méthode décrite au paragraphe E.6.2 sera encore d'un grand secours, par exemple pour prouver qu'une DF est irréductible. A noter que cette définition a pour origine une de celles qui sont proposées dans [Date 2004] :

« A relvar is in BCNF if and only if every nontrivial, left-irreducible FD has a candidate key as its determinant. »

(Unerelvar est en BCNF si et seulement si le déterminantde chaque DF non triviale, irréductible à gaucheest une clé candidate de la relvar.)

3.3.2. Théorème de Heath

On doit à Ian Heath un théorème très important (1971), que l'on mettra à profit pour normaliser :

Soit la relvar R {A, B, C} dans laquelle A, B et C sont des sous-ensembles d'attributs de R. Si R satisfait à la dépendance fonctionnelle A ➔ B, alors R est égale à la jointure de ses projections sur {A, B} et {A, C}.

Autrement dit, si R1 et R2 représentent les relvars résultant de ces projections, alors R = R1 JOIN R2 (préservation du contenu de la base de données). On dispose là d'un moyen très efficace pour décomposer une relvar non normalisée. A user sans modération (sauf si l'on autorise la présence du bonhomme NULL, cf. paragraphe D en annexe), mais tout en ayant à l'esprit la règle de préservation des dépendances :

Préservation des dépendances

On doit à Jorma Rissanen une règle importante, grâce à laquelle on évitera de perdre des DF :

Soit la relvar R {A, B, C} dans laquelle A, B et C sont des sous-ensembles d'attributs de R. Si R satisfait aux dépendances fonctionnelles A ➔ B et B ➔ C, alors plutôt que de décomposer R en {A, B} et {A, C}, on décomposera R en {A, B} et {B, C}.

En effet, en procédant ainsi, R est encore égale à la jointure de ses projections sur {A, B} et {B, C}, et surtout, on ne perd pas en route la DF B ➔ C, qui est quand même la traduction formalisée d'une règle de gestion des données.

Se reporter aussi au paragraphe E.7.2 où l'on traite plus avant de la préservation des dépendances.

3.3.3. Comment normaliser une relvar qui n'est pas en BCNF

Dans le cas de la relvar FPV (cf. Figure 3.6), pour évacuer le problème posé par la dépendance fonctionnelle {Four_No} ➔ {Ville}, si l'on a présent à l'esprit le théorème de Heath, il suffit de procéder ainsi :

1.   Définir une relvar FV, qui soit la projection de la paire {Four_No, Ville} :

         FV (Four_No, Ville)

      (par application de la définition de la clé candidate (principes d'unicité et d'irréductibilité), la clé de FV est composée du seul attribut Four_No).

2.   Définir une relvar FPQ qui soit la projection de FPV sur l'ensemble des attributs de FPV sauf Ville :

         FPQ (Four_No, Piece_No, Quantite)

En sorte que par jointure naturelle de FV et FPQ on retrouve FPV :

FPV = FV JOIN FPQ

3.3.4. Décomposition par projection - jointure préservant l'information

Ainsi, le processus de normalisation met en jeu le mécanisme de projection - jointure (naturelle) :

Par projection d'une DF qui est la cause d'un viol de BCNF, on décompose une relvar R non normalisée en deux relvars R1 et R2 (mieux, sinon totalement) normalisées.

Et l'on sait que — en vertu du théorème de Heath — par jointure naturelle des relvars R1 et R2, on retrouve la relation initiale, avec préservation du contenu de la base de données.

Cedernier point est important, car le but de l'opération est de retrouverla relation initiale dans son intégrité: la normalisation par projection/jointure (nonlossdecomposition) estune décomposition préservant l'information.
On recommence le processus tant qu'il y a encore à normaliser.

Application. Résultat de la normalisation de la relvar FPV (FPV = FV JOIN FPQ) :

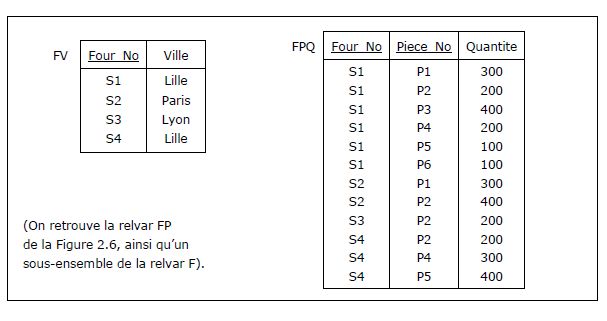
Figure 3.7 - Normalisation par décomposition de la relvar FPV

3.3.5. Normalisation et intégrité référentielle

Il est évident que lorsqu'on a normalisé en ayant tenu compte de la recommandation de Rissanen, l'intégrité référentielle doit à son tour être assurée. Ainsi, existe-t-il une contrainte de ce type entre les relvars FV et FPQ suite à la normalisation de la relvar FPV en BCNF (cf. ci-dessus) :

Version Tutorial D :

     VAR  FPQ  BASE RELATION {
               Four_No     INTEGER
             , Piece_No    INTEGER
             , Quantite     INTEGER }
         KEY {Four_No, Piece_No}
         FOREIGN KEY {Four_No}   REFERENCES  FV {Four_No} ... ;

Version SQL :

     CREATE TABLE FPQ (
               Four_No     INTEGER      NOT NULL
             , Piece_No    INTEGER      NOT NULL
             , Quantite     INTEGER      NOT NULL
         CONSTRAINT  FPQ_PK    PRIMARY KEY (Four_No, Piece_No)
         CONSTRAINT  FPQ_AK1 FOREIGN KEY (Four_No) REFERENCES  FV (Four_No) ...) ;

3.3.6. Conséquences de la normalisation par projection - jointure

Une fois achevé le travail de normalisation, on observera que :

1.    Du point de vue de la modélisation conceptuelle, tout est plus cohérent.

2.    Les problèmes de mise à jour s'arrangent.

       a.     Ainsi, on peut désormais stocker dans la base de données le fait que le fournisseur S5 réside en Arles même s'il n'a effectué aucun
               envoi (comme dans le cas de la relvar F de la Figure 2.6, dont FV est une restriction/projection).

       b.     On peut aussi supprimer les envois d'un fournisseur, tout en conservant l'information comme quoi il réside dans telle ville.

       c.     On contraint un fournisseur à résider dans une seule ville, comme cela l'a été spécifié au niveau des règles de gestion :
               Nul besoin de définir une contrainte supplémentaire à cet effet.

3.4. Deuxième et troisième formes normales

3.4.1. BCNF versus 2NF et 3NF

Chronologiquement, la BCNF (présentée en 1974) fut précédée de deux autres formes normales, dites deuxième et troisième formes normales (2NF et 3NF), décrites initialement par Ted Codd (voir [Codd 1971] par exemple).

Au fil du temps, ces deux formes normales ont été, hélas ! parfois remaniées, faussées par des mains inexpérimentées. Quoi qu'il en soit, les deuxième et troisième formes normales sont moins efficaces : la BCNF permet d'éliminer des redondances face auxquelles ses deux sœurs aînées sont impuissantes. Et puis, il serait dommage de mémoriser trois définitions quand une seule suffit, celle de la BCNF, dont l'énoncé est conceptuellement plus simple et ne fait pas référence à la panoplie complète des dépendances fonctionnelles. Qui peut le plus peut le moins :

Sur le terrain, on gagnera un temps précieux à vérifier directement la BCNF et à ne faire éventuellement appel à ses petites sœurs — moins efficaces — qu'en cas de problème, à savoir violer la BCNF pour éviter la perte d'une règle de gestion (cf. paragraphe 3.7).

3.4.2. Deuxième forme normale (2NF)

Dans son article de 1971, Ted Codd donne la définition suivante de la deuxième forme normale (2NF), dans laquelle nous conservons le terme relation, bien que celui de relvar y soit plus approprié :

Une relation R est en deuxième forme normale si elle est en première forme normale et si chaque attribut n'appartenant à aucune clé candidate est en dépendance totale de chaque clé candidate de R.

(« A relation R is in second normal form if it is in first normal form and every non-prime attribute of R is fully dependant on each candidate key of R. »)

Pour Codd, un prime attribute, est un attribut qui appartient à au moins une clé candidate de R, et a contrario, un non-prime attribute est un attribut qui n'appartient à aucune clé candidate de R (on peut préférer utiliser l'expression attribut non clé).

Rappelons qu'une dépendance fonctionnelle est totale (ou irréductible à gauche ou élémentaire) si elle n'est ni triviale ni partielle (cf. paragraphe 3.2.2).

On peut ainsi constater que la relvar FPV (Figure 3.6) n'est pas en deuxième forme normale, car l'attribut Ville n'appartient pas à la clé candidate {Four_No, Piece_No}, mais en dépend partiellement puisque {Four_No} ➔ {Ville}. Pour normaliser, on utilise une fois de plus le mécanisme de décomposition sans perte, par projection - jointure, en mettant à nouveau à profit le théorème de Heath.

Remarque importante :

Hélas, trois fois hélas ! La définition la plus courante donnée de la 2NF est la suivante :

Une relation R est en deuxième forme normale si elle est en première forme normale et si chaque attribut n'appartenant pas à la clé primaire de R est en dépendance totale de celle-ci.

Cette définition est bien sûr incomplète, car seule la clé primaire est prise en compte, tandis que les clés alternatives passent à la trappe. Il est probable qu'en se recopiant les uns les autres, les rédacteurs se sont inspirés de la définition proposée par Chris Date, mais sans tenir compte de l'avertissement que celui-ci a pourtant pris soin de donner au lecteur :

« Pour des raisons de simplicité, on supposera que chaque relation a exactement une clé candidate, c'est-à-dire une clé primaire et aucune clé alternative. »

D'où la définition donnée par Date, valable seulement dans ce cas particulier :

A relvar is in 2NF if and only if it is in 1NF and every nonkey attribute is irreducibly dependant on the primary key.

Un attribut est non clé (nonkey) quand il n'appartient pas à la clé primaire de la relvar. Nombre de ceux qui ont recopié cette définition de Date n'ont malheureusement pas lu son avertissement et feraient bien de s'inspirer de [Bouzeghoub 1990], je cite :

« Si une relation possède plusieurs clés, la définition doit être vérifiée pour chaque clé. »

A défaut, dans le cas général, cette définition de la 2NF qui ne tient compte que de la clé primaire est bien sûr trop faible : il est par exemple courant de mettre en oeuvre un attribut artificiel, utilisé pour définir la clé primaire d'une table (ceci vaut au niveau conceptuel, mutatis mutandis), admettons. C'est ce qu'on a fait pour la relvar FPVX ci-dessous, supposée remplacer la relvar FP (cf. Figure 2.6), étendue de l'attribut Ville. Mais l'ajout de l'attribut PVX_Id, fait que la paire {Four_No, Piece_No} est ravalée au rang de clé alternative (clé primaire soulignée, clé alternative en italiques) :

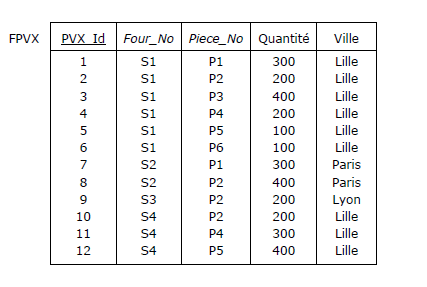
Figure 3.8 - La relvar FPVX, censée respecter 2e forme normale

PVX_Id étant le seul attribut entrant dans la composition de la clé primaire, tous les autres attributs sont en dépendance totale de celle-ci : FPVX respecte la deuxième forme normale incomplète ! Mais la redondance et les problèmes de mise à jour et autres sont toujours bien présents...

=> Bannissons la définition incomplète et utilisons celle de Codd (ou mieux, restons-en à la BCNF).

Par ailleurs, si la mise en oeuvre d'un attribut tel que PVX_Id s'avère nécessaire, ne l'envisageons que pour des relvars déjà normalisées en BCNF (ou de préférence en 5NF, car certaines erreurs pourraient encore se faufiler).

3.5. Dépendance transitive, dépendance directe

A son tour, la définition de la troisième forme normale fait intervenir un autre type de DF, à savoir la DF transitive.

Soit deux sous-ensembles d'attributs X, Y appartenant à l'en-tête H d'une relvar R, et un attribut A appartenant également à H mais n'appartenant pas à Y. La dépendance fonctionnelle X ➔ {A} est dite transitive si elle vérifie (cf. [Delobel 1982], « Normalité d'une relation ») :

(1)    X ➔ Y

(2)    Y ➔ {A}

(3)    Y

X (la dépendance fonctionnelle Y ➔ X n'existe pas)

(4) Y n'est pas inclus dans X (la dépendance fonctionnelle X ➔ Y est n'est donc pas triviale)

A contrario si {A} ne dépend pas transitivement de X, la dépendance fonctionnelle X ➔ {A} est dite directe.

3.6. Troisième forme normale (3NF)

Dans son article de 1971, Ted Codd donne cette définition de la troisième forme normale (3NF) :

Une relation R est en troisième forme normale si elle est en deuxième forme normale et si chaque attribut n'appartenant à aucune clé candidate ne dépend directement que des clés candidates de R.

(« A relation R is in third normal form if it is in second normal form and every non-prime attribute of R is non-transitively dependant on each candidate key of R. »)

Rappel : pour Codd, un prime attribute, est un attribut qui appartient à au moins une clé candidate de R, et a contrario, un non-prime attribute est un attribut qui n'appartient à aucune clé candidate de R.

La traduction littérale de la définition de Codd ne serait pas très satisfaisante, d'où un léger aménagement. Peu importe, retenons ceci : pour que la 3NF soit respectée, un attribut n'appartenant pas à une clé candidate ne doit jamais dépendre directement d'un sous-ensemble d'attributs qui ne constitue pas lui-même une clé candidate.

Une définition plus intéressante est celle de Zaniolo, car elle montre que la BCNF implique la 3NF (il suffit en effet d'y supprimer la 3e condition pour retrouver la définition de la BCNF) :

Soit R une relvar, X un sous-ensemble d'attributs de l'en-tête de R et A un attribut de cet en-tête. R est en troisième forme normale (3NF) si et seulement si, pour chaque dépendance fonctionnelle X ➔ {A} qui doit être vérifiée par R, au moins une des conditions suivantes est satisfaite :
1.  A est un élément de X (cette dépendance fonctionnelle est donc triviale).
2.  Xest une surclé de R.
3.  Aappartient à une clé candidate de R.

Bien entendu, Il existe d'autres définitions de la troisième forme normale, dont la plus courante (hélas !) est la suivante :

Une relation R est en troisième forme normale si et seulement si :
1. Elle est en deuxième forme normale ;
2. Tout attribut n'appartenant pas à la clé primaire de R n'en dépend pas transitivement.

Comme dans le cas de la 2NF non coddienne, cette définition est incomplète (et même fausse dans le cas général, cf. paragraphe 3.9), puisque cette fois-ci encore elle est muette à propos des clés alternatives. Nombre de ceux qui ont recopié la définition de Chris Date ont une fois de plus oublié de tenir compte de son avertissement :

« Pour des raisons de simplicité, on supposera que chaque relation a exactement une clé candidate, c'est-à-dire une clé primaire et aucune clé alternative. »

A titre d'exercice, on peut montrer que la relvar FPVX de la Figure 3.8 enfreint la 3NF.

En effet, au sens de Codd, la relvar enfreint la 2NF, donc a fortiori la 3NF. Mais acceptons la définition incomplète de la 2NF, selon laquelle FPVX respecterait la 2NF. Toutefois, quelle que soit la définition que l'on utilise de la 3NF, on montre que FPVX enfreint la 3NF. De fait, puisque {PVX_Id} est clé primaire, on peut mettre en évidence les DF suivantes :

      DF1 :  {PVX_Id} ➔ {Four_No}

      DF2 :  {PVX_Id} ➔ {Piece_No}

      DF3 :  {PVX_Id} ➔ {Quantite}

      DF4 :  {PVX_Id} ➔ {Ville}

Pour être complet, comme {Four_No, Piece_No} est clé alternative, on a aussi :

      DF5 :  {Four_No, Piece_No} ➔ {PVX_Id}

      DF6 :  {Four_No, Piece_No} ➔ {Quantite}

      DF7 :  {Four_No, Piece_No} ➔ {Ville}

En utilisant la règle d'union inférée des axiomes d'Armstrong (cf. paragraphe E en annexe), de DF1 et DF2, on produit la DF :

      DF8 :  {PVX_Id} ➔ {Four_No, Piece_No}

Il existe aussi la DF à l'origine de l'infraction :

      DF9 :  {Four_No} ➔ {Ville}

La relvar FPVX n'est pas en 3NF, puisqu'en fait DF4 peut être obtenue à partir de DF1 et DF9 (axiome d'Armstrong de transitivité), c'est-à-dire que l'attribut Ville qui n'appartient pas à la clé primaire {PVX_Id} de la relvar, dépend transitivement de cette clé, via le singleton {Four_No} qui lui-même n'est pas clé.

Conclusion :

N'utiliserque les définitions de Codd de la 2NF et dela 3NF (on peut aussi préférer Zaniolo), oucelles qui lui sont équivalentes (cf. par exemple [Delobel 1982], [Gardarin 1988]), et d'urgence mettre à la poubelle celles quise limitent aux clésprimaires.
Mieuxencore : dans le travail de normalisation, au nom du rasoir d'Ockham, prendre l'habitude de laisser tomberla 2NF et la 3NF, au profit de la seule BCNF. On peut aussi arguer de ce choixsi l'on est limité par le temps, un peu paresseuxet doté d'une mémoire assez volatile pour ne pas retenir toutes lesdéfinitions.

Ainsi, dans le cas de l'exercice qui vient d'être proposé, sans perdre de temps à vérifier la 2NF puis la 3NF avant d'en arriver à la BCNF, le diagnostic est rapide et le remède simple et efficace :

Le déterminant {Four_No} de la DF non triviale DF9 n'étant pas une surclé de la relvar FPVX, celle-ci enfreint la BCNF et il faut la décomposer. Pour cela, on applique le théorème de Heath, sans oublier la règle de Rissanen de préservation des dépendances (cf. paragraphe 3.3.2).

Procédons ainsi, en représentant d'abord la relvar FPVX sous la forme suivante :

      FPVX { {Four_No}, {Ville}, {PVX_Id, Piece_No, Quantite} }

Puisque l'on a la DF {Four_No} ➔ {Ville}, la relvar peut être ainsi décomposée (avec préservation des DF) :

      FPVXa {Four_No, Ville}

      FPVXb {Four_No, PVX_Id, Piece_No, Quantite}

FPVXan'est jamais que la projection sur les attributs Four_No et Ville dela relvar F (Figure 2.6), et comme elle n'en est qu'un sous-ensemble elle peutdisparaître.

FPVXbn'est jamais que de la relvar FP (Figure 2.6) ayant subi une extension (ajoutde l'attribut PVX_Id). En fait, l'attribut PVX_Id n'apporte strictement rien au plande la modélisation et des opérations: au nom du rasoir d'Ockham, il doit passer à la trappe, à la suite de quoi on retrouveFP.

3.7. Un problème embarrassant de BCNF

On peut être confronté au dilemme suivant :

Si une relvar n'est pas en BCNF, par application du théorème de Heath, on sait la décomposer sans perte, mais il y a un hic : on pourrait ne pas respecter la règle de préservation des dépendances (cf. paragraphe 3.3.2 et annexe E.7.2), c'est-à-dire qu'en décomposant, on perdrait une DF et par voie de conséquence, la règle de gestion dont cette DF est issue ne serait plus garantie. Le remède peut être pire que le mal. Que faire ?

Illustrons ceci à l'aide d'un exemple proposé par Chris Date (cf. [Date 2004], page 370), en considérant la relvar EMP suivante (francisée) :

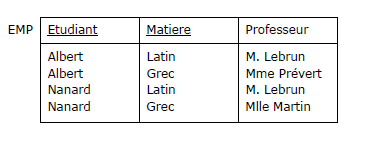
Figure 3.9 - Relvar EMP

Règles de gestion extraites du corpus des règles consignées dans le dossier de conception qui nous a été transmis :

      (R1)     Pour chaque matière étudiée par un étudiant, celui-ci n'a qu'un professeur.

      (R2)     Chaque professeur n'enseigne qu'une matière.

      (R3)     Chaque matière peut être enseignée par plusieurs professeurs.

      (R4)     Chaque professeur peut enseigner sa matière à plusieurs étudiants.

       ...       Etc.

Traduction sous forme de dépendances fonctionnelles :

      DF1 :  {Etudiant, Matiere} ➔ {Professeur}

      DF2 :  {Professeur} ➔ {Matiere}

La relvar EMP ne respecte pas la BCNF, car le déterminant {Professeur} de DF2 n'est pas une surclé, un professeur pouvant avoir plusieurs étudiants (par exemple, M. Lebrun a au moins deux étudiants, Albert et Nanard).

On normalise en appliquant le théorème de Heath sur la base de DF2, en décomposant donc ainsi la relvar EMP :

      PM {Professeur, Matière}              ayant pour seule clé candidate {Professeur}.

      PE {Professeur, Etudiant}              ayant pour seule clé candidate {Professeur, Etudiant}.

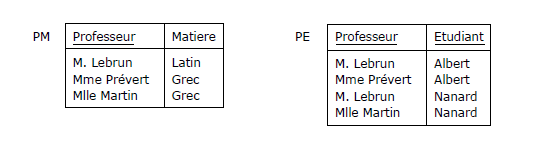
Figure 3.10 - Projection de EMP selon PM et PE

Ces deux relvars sont en BCNF, l'information est préservée, mais on perd DF1, donc la règle de gestion (R1), et si Mlle Martin enseigne le grec à Nanard, rien n'empêcherait désormais que Mme Prévert lui enseignât aussi cette matière...

Alors faut-il violer la BCNF ?

On peut effectivement préférer ne pas décomposer la relvar EMP et se limiter au respect de la 3NF, mais en contrepartie il faudra prévoir une contrainte garantissant le respect de la dépendance fonctionnelle DF2, comme quoi un professeur n'enseigne qu'une matière.

Dans le style de Tutorial D :

     VAR EMP BASE RELATION {Etudiant CHAR, Matiere CHAR, Professeur CHAR}
         KEY {Etudiant, Matiere} ;

     CONSTRAINT EMPDF2
         FORALL x, y

EMP (x.Professeur = y.Professeur ⇒ x.Matiere = y.Matiere) ;

(La contrainte se lit ainsi : Quels que soient les tuples x et y de la relvar EMP, si x.Professeur = y.Professeur alors x.Matiere = y.Matiere)

Version SQL :

A défaut, à la place de l'assertion SQL, on peut utiliser une vue munie d'une clause WITH CHECK OPTION :

Mais il faudra interdire l'accès à la table EMP pour les opérations de mise à jour et n'autoriser en l'occurrence que l'utilisation de la vue, système manquant un peu de souplesse. Quoi qu'il en soit, on peut aussi se rabattre sur un trigger SQL pour garantir la dépendance fonctionnelle DF2.

Exemple avec SQL Server 2005 :

Et bien entendu, il faudra prévoir un trigger pour contrôler les nouvelles valeurs prises par les attributs Matiere et Professeur lors des opérations d'update portant sur ces attributs.

Concernant les opérations d'INSERT, on peut désormais violer la BCNF, puisque l'on sait faire respecter la DF {Professeur} ➔ {Matiere}.

Pour le reste, il y a quand même un hic, car si Nanard n'étudie pas le grec mais le sanscrit, remplacer le tuple <"Nanard", "Grec", "Mlle Martin"> par le tuple <"Nanard", "sanscrit", "M. Antoun"> a pour effet que l'on perd l'information selon laquelle Mlle Martin enseigne le grec si Nanard était son seul élève dans cette matière. Il sera prudent de commencer par le commencement, c'est-à-dire produire un MCD (ou un diagramme de classes), dans lequel figurent les entités-types Professeur, Matiere, Etudiant, une association-type entre Professeur et Matiere, une association-type ternaire, à savoir EMP, entre les trois entités-types et une CIF (contrainte d'intégrité fonctionnelle) entre EMP et Professeur. Une fois cette tâche accomplie, alors seulement on pourra dériver le MCD : il s'agit là du processus normal de conception d'une base de données.

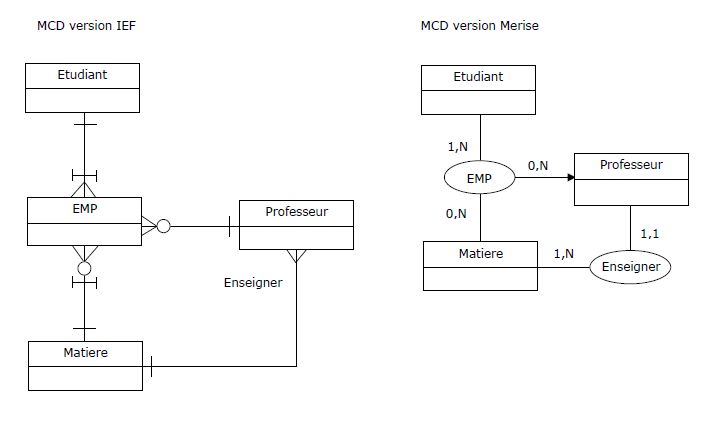
Figure 3.11 - Relvar EMP - Vision conceptuelle

En redescendant au niveau relationnel, on devra s'occuper des pièges qui seront immanquablement tendus. Par exemple, si le corps de la relvar EMP contient le tuple <"Nanard", "Grec", "Mlle Martin">, après tout la matière enseignée par Mlle Martin peut très bien être le solfège... On part pour un trigger supplémentaire (ou une « surclé étrangère » inavouable entre EMP et Professeur...) pour s'assurer que la matière enseignée par un professeur aux élèves est bien celle que ce professeur est réputé enseigner.

Alors faut-il respecter la BCNF ?

En réaction à ce qui précède, normaliser et mettre en oeuvre les relvars PM {Professeur, Matière} et PE {Professeur, Etudiant} semble s'imposer, avec toutefois un contrôle à assurer pour la dépendance fonctionnelle DF1 {Etudiant, Matiere} ➔ {Professeur} puisque celle-ci est perdue après projection.

Par contre, sémantiquement parlant, le MCD correspondant ne ressemble pas à grand-chose, et respecter la BCNF n'est finalement peut-être pas ici ce qu'il y a de mieux...

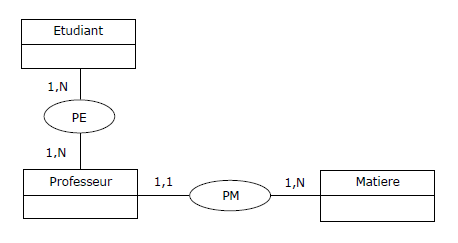
Figure 3.12 - Relvar EMP - Vision conceptuelle, variante

On est forcé d'en convenir. En tout cas, le code correspondant est le suivant :

Dans le style de Tutorial D :

     VAR PM BASE RELATION {Professeur CHAR, Matiere CHAR}
         KEY {Professeur} ;

     VAR PE BASE RELATION {Professeur CHAR, Etudiant CHAR}
         KEY {Professeur, Etudiant}
         FOREIGN KEY {Professeur} REFERENCES PM ;

     CONSTRAINT EMPDF1
         FORALL x, y

(PE JOIN PM) (x.Etudiant = y.Etudiant AND x.Matiere = y.Matiere ⇒ x.Professeur = y.Professeur) ;

Version SQL :

Etc.

3.8. Retour sur la dénormalisation a priori

Le thème de la dénormalisation a été abordé au paragraphe 1.6. Voici comment en termes choisis on propage un mythe sans manifestement être allé vérifier comment se passent concrètement les choses. Je cite à nouveau le redoutable [RoMo 1989] qui écrit à la page 198 de l'ouvrage, sous le titre « Optimisation du MLD relationnel » :

« Une optimisation structurelle principale peut être effectuée au niveau logique, il s'agit de la création d'une certaine redondance en vue de diminuer le nombre d'actions élémentaires nécessaires à la satisfaction d'une requête en diminuant notamment le nombre de jointures entre tuples différents... »

Et l'auteur fournit un exemple de MLD dans lequel une table initialement en BCNF (en fait 5NF) viole désormais la 3NF, suite à injection d'une DF transitive (cf. paragraphe 3.5). Un avion (table Avion) est d'un certain type (table TypeAvion, porteuse d'un attribut NombreDePlaces) : la recommandation est de dupliquer l'attribut NombreDePlaces dans la table Avion. Cela part d'une bonne intention, l'auteur évoquant la possibilité « qu'il soit souvent demandé quelle est la capacité d'un avion ». Mais il aurait dû parler des effets secondaires et insister sur les précautions élémentaires à prendre avant de nous laisser nous embarquer dans ce genre de galère : prototyper et quantifier les performances, mettre en œuvre une contrainte sous-traitée au SGBD pour garantir en toute sécurité la cohérence des valeurs prises par l'attribut NombreDePlaces dans les deux tables concernées... Bref, l'imprudent aurait surtout dû conclure que les concepteurs et les développeurs doivent s'en remettre aux DBA, lesquels sont outillés pour juger objectivement de l'(in)efficacité de la dénormalisation : ficher une zoubia pas possible pour se « satisfaire » d'un gain qui sera peut-être de l'ordre de la milliseconde ?

L'enfer est pavé de bonnes intentions. Allons-y d'un contre-exemple.

Dans une banque d'une ville méridionale où il fait bon vivre. On me soumet le problème suivant : Les chèques des clients sont regroupés en remises, lesquelles sont à leur tour regroupées en lots. Tous les chèques datés du tant doivent être supprimés de la table des chèques. Manque de chance, l'attribut de type Date utilisé pour l'opération de restriction ne figure pas dans la table Cheque, mais dans la table « grand-parente », Lot (attribut LotDate).

Ce qui est embêtant dans cette affaire, c'est que le traitement (hebdomadaire) dure près de 9 heures, pour une table de 2 millions de chèques (d'accord, ça se passait en 1993, mais quand même...) A l'unanimité moins une voix, celle de votre serviteur, le verdict tomba : « C'est la faute à la 3NF, il faut dé-nor-ma-lis-er ! »

Structure des tables :

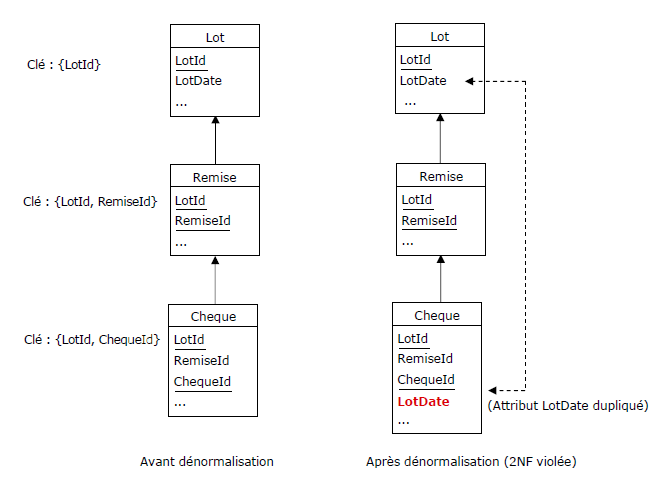
Figure 3.13 - Dénormalisation de la table des chèques

Requêtes de suppression des chèques :

Dénormaliser est certes bien tentant, mais avant que l'on ne commette le viol (en fait celui de la 2NF dans cet exemple), avant restructuration de la table Cheque, avant que ne soit aménagé le programme de suppression des chèques, etc., j'ai demandé que fut mesuré le coût du seul SELECT : celui-ci était de l'ordre de deux minutes. Stupeur des accusateurs ! La jointure, cette présumée coupable était lavée de tous les soupçons (son surcoût était infime, de l'ordre de quelques secondes). En fait, la table Cheque était lourdement lestée de cinq index que le SGBD (à savoir DB2) devait mettre à jour eux aussi (dont un du reste ne servait strictement à rien). La solution était donc évidente : ne pas dénormaliser, et avant d'exécuter le traitement de suppression des chèques, commencer par « dropper » les index (sauf l'index cluster qui s'avérait peu pénalisant, par contraste avec les autres index qui étaient tous à l'origine de très nombreuses lectures/écritures de pages physiques, sans compter la journalisation), puis une fois l'opération de suppression proprement dite terminée, recréer les index. Pour une fenêtre batch autorisée de 1h30, le temps de traitement, y-compris une réorganisation de la table et la création des index, n'excéda plus une quinzaine de minutes, et l'irréparable ne fut pas commis...

Moralité : avant de dire et (faire) faire des bêtises, et se retrouver au point de départ, en ayant gagné une poignée de secondes sur 9 heures après avoir dénormalisé, on vérifie concrètement et on prouve. Bon d'accord, j'ai pris un exemple édifiant, mais j'en ai bien d'autres.

Mais attention, rien n'est jamais acquis...

Trois ans plus tard, le même problème se pose, mais cette fois-ci dans une banque située en Normandie. Fort de mon expérience méridionale, je prépare sereinement un travail de prototypage, dans les règles de l'art. Avant de faire le ménage dans la table des chèques, allons-y pour « dropper » les index qui peuvent l'être. Ceci fait, mesurons la durée de l'opération de suppression. Surprise ! Vérité en deçà des Alpilles, erreur au delà... Il se trouve que de la table des chèques dépendent d'autres tables, et que le pourcentage de chèques à supprimer est cette fois-ci beaucoup plus important, ce qui fait que l'ensemble des pages des table spaces et index spaces (fichiers DB2) est à mettre à jour, et dans ces conditions la performance attendue n'est pas au rendez-vous. Mais si on échoue par la face Nord, reste la face Sud : plutôt que supprimer, on crée. En l'occurrence, cela consista à décharger seulement les lignes à ne pas supprimer puis à les recharger dans la table en cause et dans ses tables « filles ». Ouf... Quoi qu'il en soit, une fois de plus, la normalisation était bien sûr totalement étrangère au problème de performance, mais elle aurait bien trouvé des accusateurs, ainsi qu'un folliculaire pour entretenir le mythe dans la presse du cœur informatique.

3.9. Une relvar respectant la BCNF peut-elle violer la 3NF ?

Une relvar en BCNF est nécessairement en 3NF, mais si on se sert de la définition non coddienne figurant au paragraphe 3.6, alors on peut arriver à une contradiction, à savoir qu'une relvar respectant la BCNF peut violer la 3NF. Rappelons cette définition incomplète et peccamineuse :

La contradiction peut être montrée à partir d'exemples très simples, tels que celui-ci :

Soit une relvar R {A, B, C} où A, B et C sont des attributs, et les dépendances fonctionnelles :

      DF1 :    {A} ➔ {B}

      DF2 :    {A} ➔ {C}

      DF3 :    {B} ➔ {A}

      DF4 :    {B} ➔ {C}

Ce sont les seules DF non triviales et leurs déterminants {A} et {B} sont clés candidates : R respecte la BCNF. Mais si l'on choisit par exemple {A} pour clé primaire, puisque {A} détermine {C} transitivement, la 3NF incomplète est violée. En effet :

       {A} ➔ {B} et {B} ➔ {C}  =>  {A} ➔ {C}

Parce qu'incomplète, la définition de la 3NF est fausse. Mais pour varier les plaisirs et l'occasion faisant le larron, profitons d'un exercice récapitulatif pour mettre à nouveau la contradiction en évidence. Intéressons-nous pour cela aux courses hippiques (courses de plat, galop). Ainsi, le prix de l'Arc de Triomphe, édition 2009, doté de 4 000 000 d'euros a eu lieu le 4 octobre 2009 et a vu la victoire de Sea The Stars, monté par Michael Kinane. L'édition 2010, dotée à nouveau de 4 000 000 d'euros, a vu la victoire de Workforce, monté par Ryan-Lee Moore, etc.

Définissons une table des courses et une table des partants :

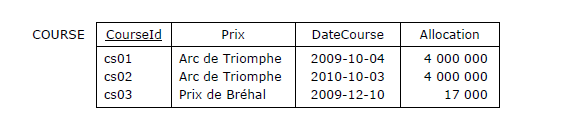
Figure 3.14 - Extrait de la table des courses hippiques

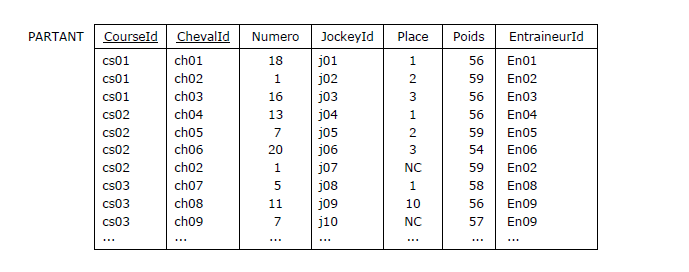
Figure 3.15 - Extrait de la table des partants

Dans la course cs01, Le cheval ch01, porteur du numéro 18, était monté par le jockey j01, il a fini à la 1re place, il portait 56 kilos et était entraîné par l'entraîneur En01, etc. A noter que dans la course cs02, le cheval ch02 a terminé non classé, alors que l'année d'avant, dans le même Prix (Arc de Triomphe), il avait fini 2e.

Intéressons nous aux dépendances fonctionnelles de la relvar PARTANT. Dans une couse donnée, un cheval ne porte qu'un numéro, il n'est monté que par un seul jockey, il termine exactement à une place, il porte exactement un poids et n'a qu'un entraîneur. On peut donc inférer la DF :

      DF01 :     {CourseId, ChevalId} ➔ {Numero, JockeyId, Place, Poids, EntraineurId}

En appliquant à cette DF l'axiome d'augmentation (cf. Annexe E.2), on infère la DF :

      DF02 :     {CourseId, ChevalId} ➔ {CourseId, ChevalId, Numero, JockeyId, Place, Poids, EntraineurId}

En conséquence quoi le déterminant {CourseId, ChevalId} de cette DF est clé candidate de la relvar.

De la même façon, dans une course donnée, un jockey ne monte qu'un cheval :

      DF03 :     {CourseId, JockeyId} ➔ {ChevalId}

En appliquant à son tour à cette DF l'axiome d'augmentation, on infère la DF :

      DF04 :     {CourseId, JockeyId} ➔ {CourseId, ChevalId}

En ce qui concerne le numéro porté par le cheval :

      DF05 :     {CourseId, Numero} ➔ {ChevalId}

En appliquant là encore à cette DF l'axiome d'augmentation, on infère la DF :

      DF06 :     {CourseId, Numero} ➔ {CourseId, ChevalId}

Et en appliquant l'axiome de transitivité, on infère les DF :

      DF07 :     {CourseId, JockeyId} ➔ {CourseId, ChevalId, Numero, JockeyId, Place, Poids, EntraineurId}

      DF08 :     {CourseId, Numero} ➔ {CourseId, ChevalId, Numero, JockeyId, Place, Poids, EntraineurId}

Ainsi, les paires {CourseId, JockeyId} et {CourseId, Numero} sont aussi clés candidates. Par ailleurs, il n'existe pas d'autres DF non triviales que celles que l'on a énumérées (deux ou plusieurs chevaux peuvent partager la même place dans la même course : ex-æquo, non classé, non partant ; un entraîneur peut avoir deux ou plusieurs chevaux engagés dans la même course, etc.)

=>    Le déterminant de chaque DF non triviale est clé candidate de la relvar : celle-ci respecte la BCNF.

Maintenant, quelle que soit la clé candidate que l'on retient pour être clé primaire, par exemple la paire {CourseId, ChevalId}, en l'occurrence on vérifie :

      DF09 :     {CourseId, ChevalId} ➔ {CourseId, JockeyId}

Mais aussi :

      DF10 :     {CourseId, JockeyId} ➔ {Place, Poids, EntraineurId}

Donc par transitivité :

      DF11 :     {CourseId, ChevalId} ➔ {Place, Poids, EntraineurId}

Autrement dit, alors que la relvar respecte la BCNF, selon la définition incomplète et peccamineuse de la 3NF, celle-ci est violée, en contradiction avec la règle selon laquelle toute relvar respectant la BCNF respecte nécessairement la 3NF :

La définition incomplète et peccamineuse est donc fausse et bonne pour la poubelle.

S'il fallait la suivre, par application du théorème de Heath, la relvar PARTANT donnerait lieu à un ensemble de relvars tel que celui-ci :

      PARTANT01 {CourseId, ChevalId, Place, Poids, EntraineurId}

      PARTANT02 {CourseId, ChevalId, Numero}

      PARTANT03 {CourseId, ChevalId, JockeyId}

Ces structures désormais « 3NF » peuvent être intéressantes, mais elles relèvent plutôt de l'optimisation de la relvar initiale PARTANT (cf. paragraphe 1.7).

Pour conclure et marquer un temps de repos bien mérité, citons Pierre Dac (1893-1975) :

« Gloire à ceux qui ont forgé silencieusement mais efficacement le fier levain qui, demain ou après-demain au plus tard, fera germer le grain fécond du ciment victorieux, au sein duquel, enfin, sera ficelée, entre les deux mamelles de l'harmonie universelle, la prestigieuse clef de voûte qui ouvrira à deux battants la porte cochère d'un avenir meilleur sur le péristyle d'un monde nouveau ! »

Fermez le ban.

N.B. J'avoue ne pas savoir si la prestigieuse clef de voûte dont parle notre cher Dac est candidate, primaire, alternative, étrangère ou autre, libre à chacun de se faire son opinion. En tout cas, gloire à Codd, Date, Darwen, et tous ceux qui ont forgé le fier levain relationnel !

Précédent Sommaire Suivant